Controlling Commercial Cooling Systems Using Reinforcement Learning

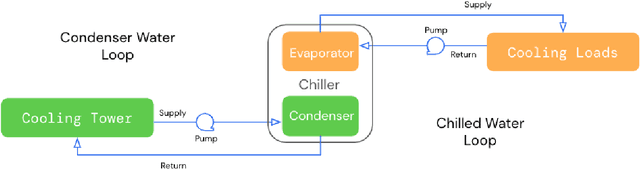
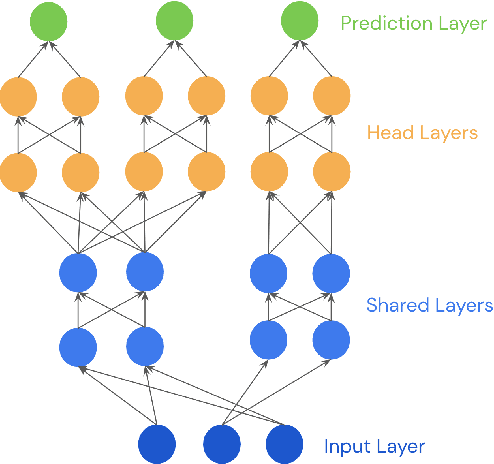
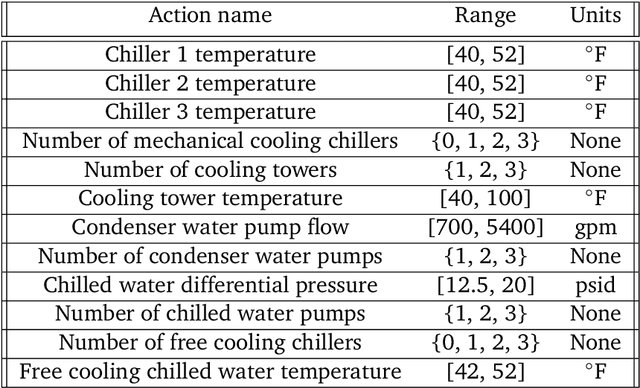
This paper is a technical overview of DeepMind and Google's recent work on reinforcement learning for controlling commercial cooling systems. Building on expertise that began with cooling Google's data centers more efficiently, we recently conducted live experiments on two real-world facilities in partnership with Trane Technologies, a building management system provider. These live experiments had a variety of challenges in areas such as evaluation, learning from offline data, and constraint satisfaction. Our paper describes these challenges in the hope that awareness of them will benefit future applied RL work. We also describe the way we adapted our RL system to deal with these challenges, resulting in energy savings of approximately 9% and 13% respectively at the two live experiment sites.

Optimizing Industrial HVAC Systems with Hierarchical Reinforcement Learning

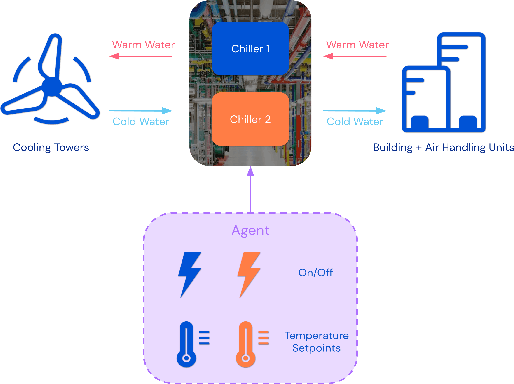
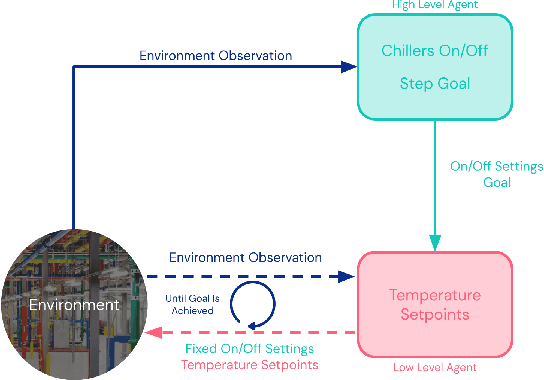
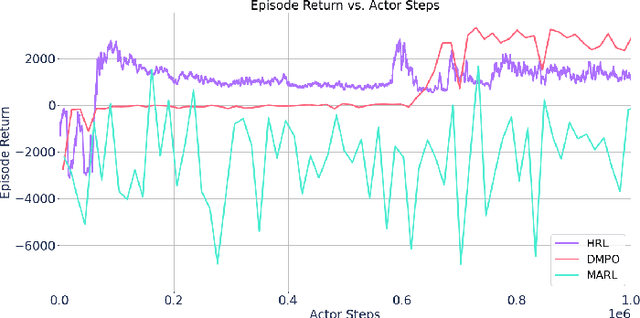
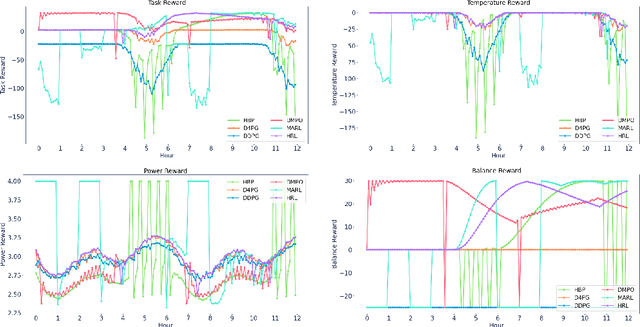
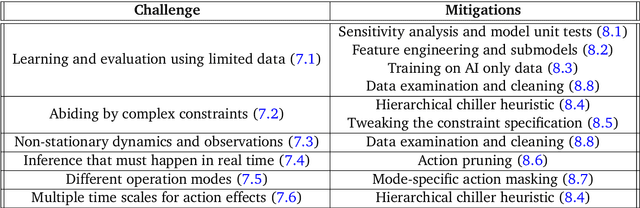
Reinforcement learning (RL) techniques have been developed to optimize industrial cooling systems, offering substantial energy savings compared to traditional heuristic policies. A major challenge in industrial control involves learning behaviors that are feasible in the real world due to machinery constraints. For example, certain actions can only be executed every few hours while other actions can be taken more frequently. Without extensive reward engineering and experimentation, an RL agent may not learn realistic operation of machinery. To address this, we use hierarchical reinforcement learning with multiple agents that control subsets of actions according to their operation time scales. Our hierarchical approach achieves energy savings over existing baselines while maintaining constraints such as operating chillers within safe bounds in a simulated HVAC control environment.

Semi-analytical Industrial Cooling System Model for Reinforcement Learning

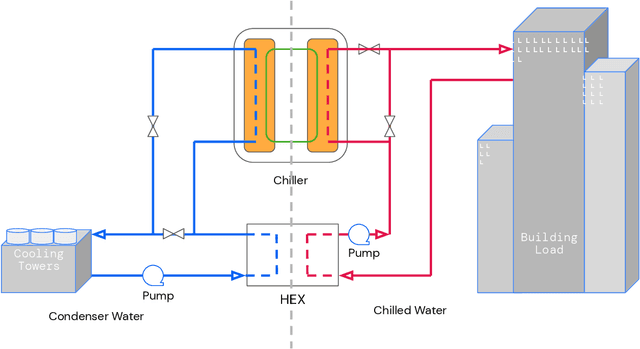
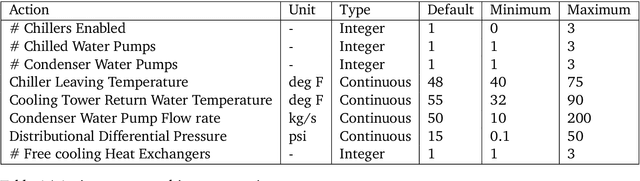
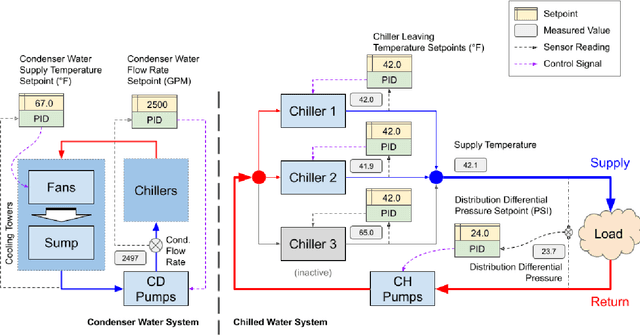
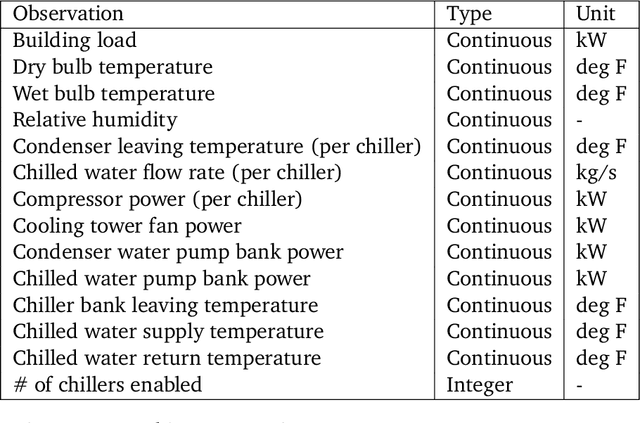
We present a hybrid industrial cooling system model that embeds analytical solutions within a multi-physics simulation. This model is designed for reinforcement learning (RL) applications and balances simplicity with simulation fidelity and interpretability. The model's fidelity is evaluated against real world data from a large scale cooling system. This is followed by a case study illustrating how the model can be used for RL research. For this, we develop an industrial task suite that allows specifying different problem settings and levels of complexity, and use it to evaluate the performance of different RL algorithms.

Practical Algorithms for Learning Near-Isometric Linear Embeddings

We propose two practical non-convex approaches for learning near-isometric, linear embeddings of finite sets of data points. Given a set of training points $\mathcal{X}$, we consider the secant set $S(\mathcal{X})$ that consists of all pairwise difference vectors of $\mathcal{X}$, normalized to lie on the unit sphere. The problem can be formulated as finding a symmetric and positive semi-definite matrix $\boldsymbol{\Psi}$ that preserves the norms of all the vectors in $S(\mathcal{X})$ up to a distortion parameter $\delta$. Motivated by non-negative matrix factorization, we reformulate our problem into a Frobenius norm minimization problem, which is solved by the Alternating Direction Method of Multipliers (ADMM) and develop an algorithm, FroMax. Another method solves for a projection matrix $\boldsymbol{\Psi}$ by minimizing the restricted isometry property (RIP) directly over the set of symmetric, postive semi-definite matrices. Applying ADMM and a Moreau decomposition on a proximal mapping, we develop another algorithm, NILE-Pro, for dimensionality reduction. FroMax is shown to converge faster for smaller $\delta$ while NILE-Pro converges faster for larger $\delta$. Both non-convex approaches are then empirically demonstrated to be more computationally efficient than prior convex approaches for a number of applications in machine learning and signal processing.