Shenyinying Tu
Provably Efficient Reinforcement Learning for Online Adaptive Influence Maximization
Jun 29, 2022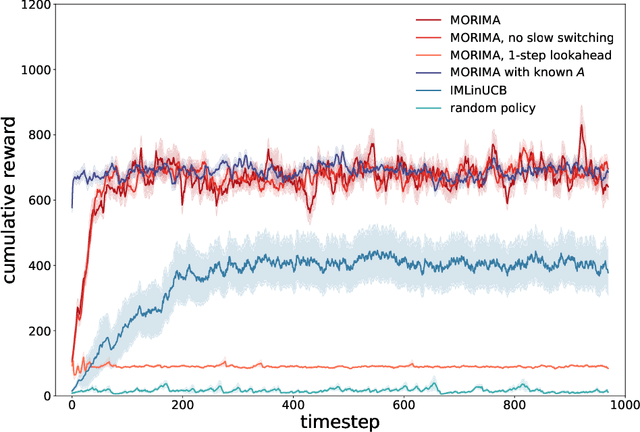
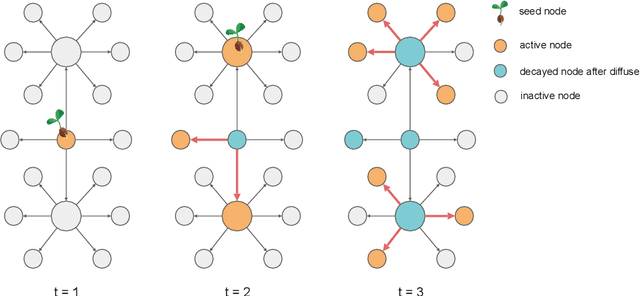
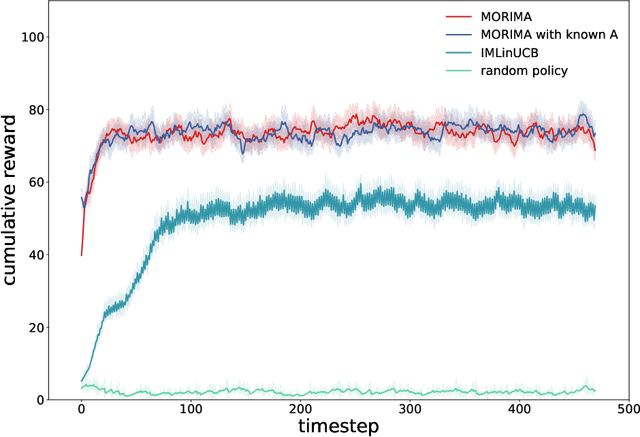
Abstract:Online influence maximization aims to maximize the influence spread of a content in a social network with unknown network model by selecting a few seed nodes. Recent studies followed a non-adaptive setting, where the seed nodes are selected before the start of the diffusion process and network parameters are updated when the diffusion stops. We consider an adaptive version of content-dependent online influence maximization problem where the seed nodes are sequentially activated based on real-time feedback. In this paper, we formulate the problem as an infinite-horizon discounted MDP under a linear diffusion process and present a model-based reinforcement learning solution. Our algorithm maintains a network model estimate and selects seed users adaptively, exploring the social network while improving the optimal policy optimistically. We establish $\widetilde O(\sqrt{T})$ regret bound for our algorithm. Empirical evaluations on synthetic network demonstrate the efficiency of our algorithm.
A Primer on Coordinate Descent Algorithms
Jan 12, 2017



Abstract:This monograph presents a class of algorithms called coordinate descent algorithms for mathematicians, statisticians, and engineers outside the field of optimization. This particular class of algorithms has recently gained popularity due to their effectiveness in solving large-scale optimization problems in machine learning, compressed sensing, image processing, and computational statistics. Coordinate descent algorithms solve optimization problems by successively minimizing along each coordinate or coordinate hyperplane, which is ideal for parallelized and distributed computing. Avoiding detailed technicalities and proofs, this monograph gives relevant theory and examples for practitioners to effectively apply coordinate descent to modern problems in data science and engineering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge