On the fast convergence of minibatch heavy ball momentum
Paper and Code
Jun 15, 2022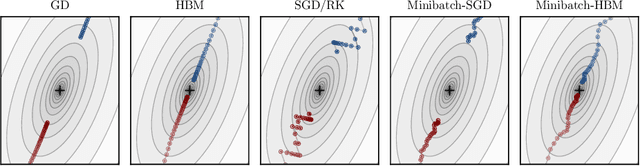
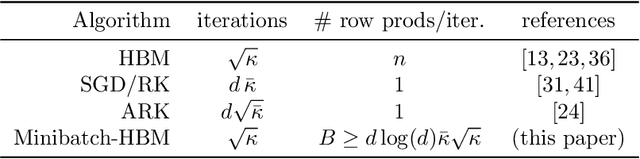
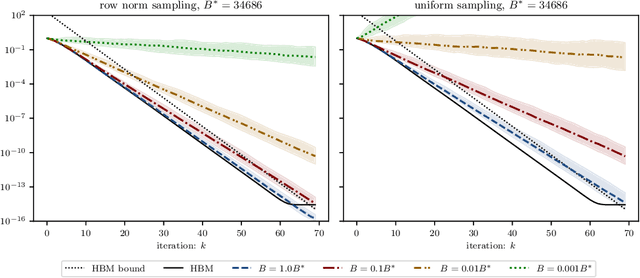
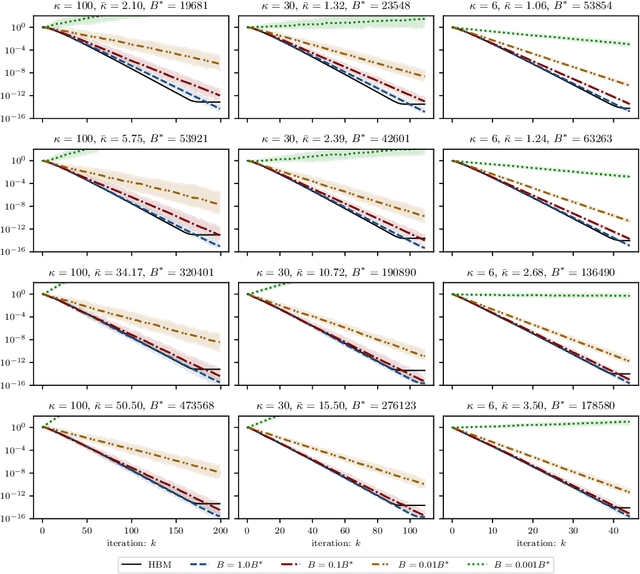
Simple stochastic momentum methods are widely used in machine learning optimization, but their good practical performance is at odds with an absence of theoretical guarantees of acceleration in the literature. In this work, we aim to close the gap between theory and practice by showing that stochastic heavy ball momentum, which can be interpreted as a randomized Kaczmarz algorithm with momentum, retains the fast linear rate of (deterministic) heavy ball momentum on quadratic optimization problems, at least when minibatching with a sufficiently large batch size is used. The analysis relies on carefully decomposing the momentum transition matrix, and using new spectral norm concentration bounds for products of independent random matrices. We provide numerical experiments to demonstrate that our bounds are reasonably sharp.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge