Constrained and Composite Optimization via Adaptive Sampling Methods

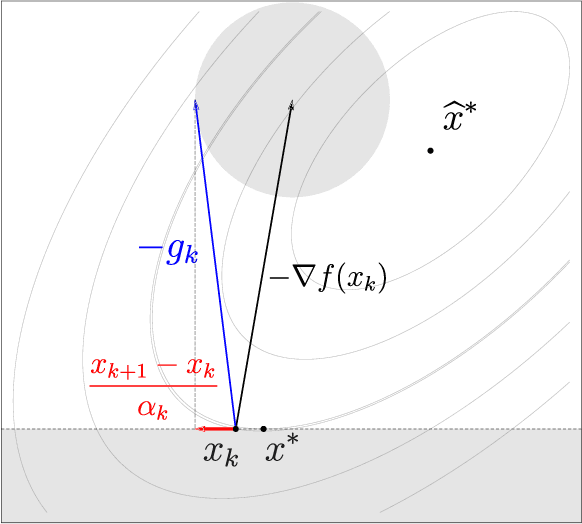
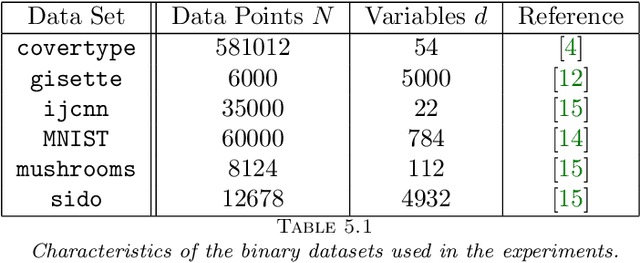
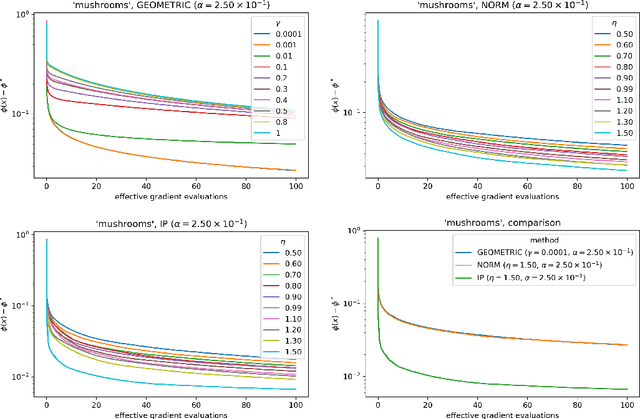
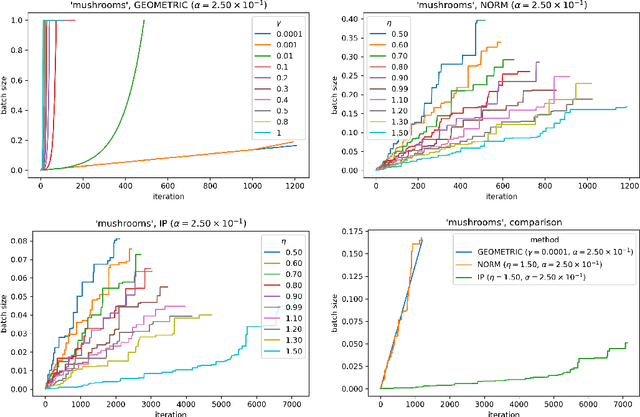
The motivation for this paper stems from the desire to develop an adaptive sampling method for solving constrained optimization problems in which the objective function is stochastic and the constraints are deterministic. The method proposed in this paper is a proximal gradient method that can also be applied to the composite optimization problem min f(x) + h(x), where f is stochastic and h is convex (but not necessarily differentiable). Adaptive sampling methods employ a mechanism for gradually improving the quality of the gradient approximation so as to keep computational cost to a minimum. The mechanism commonly employed in unconstrained optimization is no longer reliable in the constrained or composite optimization settings because it is based on pointwise decisions that cannot correctly predict the quality of the proximal gradient step. The method proposed in this paper measures the result of a complete step to determine if the gradient approximation is accurate enough; otherwise a more accurate gradient is generated and a new step is computed. Convergence results are established both for strongly convex and general convex f. Numerical experiments are presented to illustrate the practical behavior of the method.

Adaptive Sampling Strategies for Stochastic Optimization

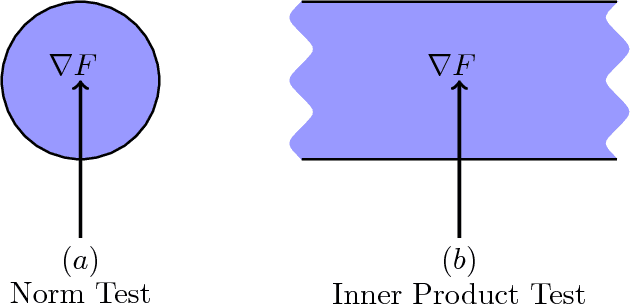
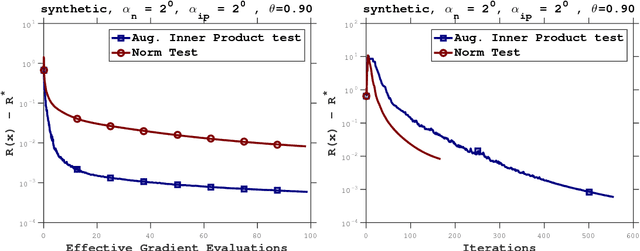
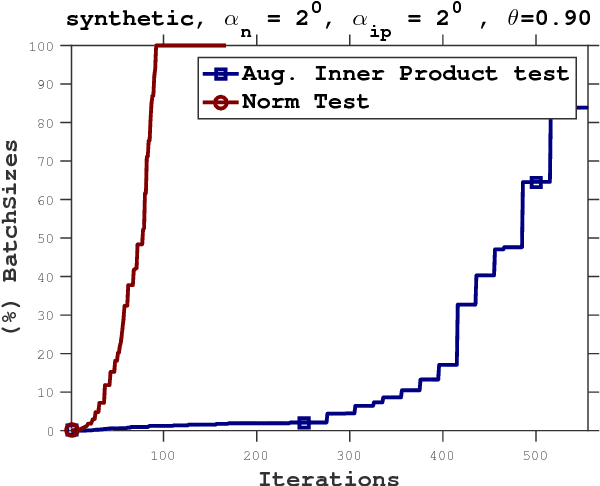
In this paper, we propose a stochastic optimization method that adaptively controls the sample size used in the computation of gradient approximations. Unlike other variance reduction techniques that either require additional storage or the regular computation of full gradients, the proposed method reduces variance by increasing the sample size as needed. The decision to increase the sample size is governed by an inner product test that ensures that search directions are descent directions with high probability. We show that the inner product test improves upon the well known norm test, and can be used as a basis for an algorithm that is globally convergent on nonconvex functions and enjoys a global linear rate of convergence on strongly convex functions. Numerical experiments on logistic regression problems illustrate the performance of the algorithm.

Exact and Inexact Subsampled Newton Methods for Optimization

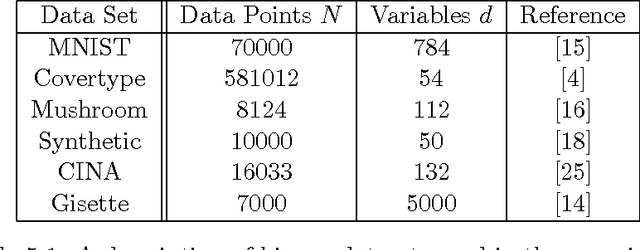
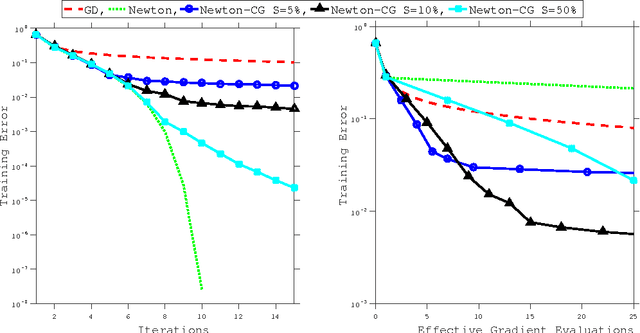
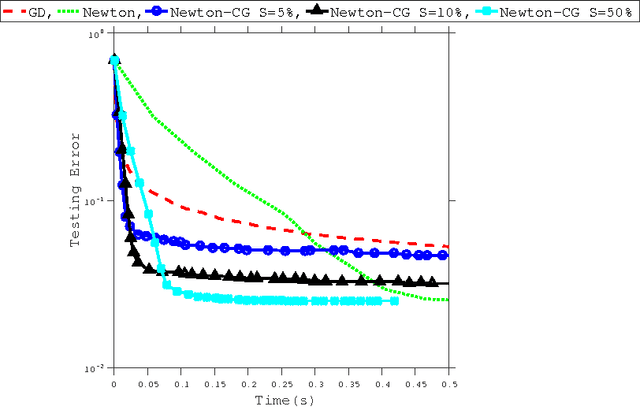
The paper studies the solution of stochastic optimization problems in which approximations to the gradient and Hessian are obtained through subsampling. We first consider Newton-like methods that employ these approximations and discuss how to coordinate the accuracy in the gradient and Hessian to yield a superlinear rate of convergence in expectation. The second part of the paper analyzes an inexact Newton method that solves linear systems approximately using the conjugate gradient (CG) method, and that samples the Hessian and not the gradient (the gradient is assumed to be exact). We provide a complexity analysis for this method based on the properties of the CG iteration and the quality of the Hessian approximation, and compare it with a method that employs a stochastic gradient iteration instead of the CG method. We report preliminary numerical results that illustrate the performance of inexact subsampled Newton methods on machine learning applications based on logistic regression.