Dynamic social learning under graph constraints
Paper and Code
Jul 08, 2020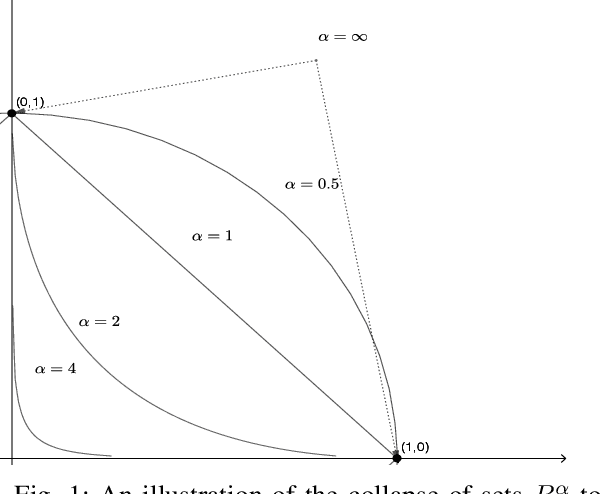
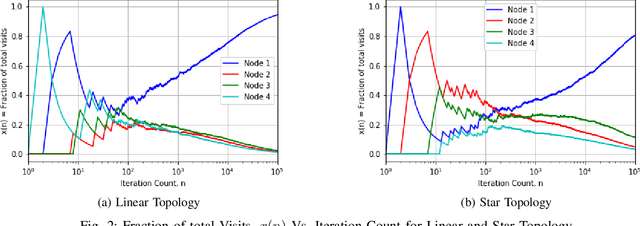
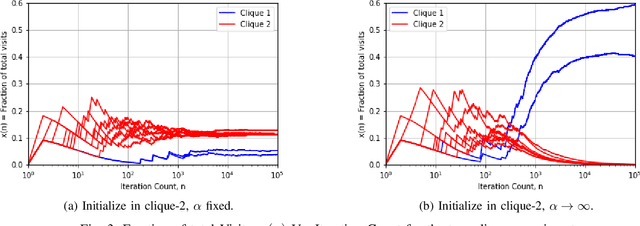
We argue that graph-constrained dynamic choice with reinforcement can be viewed as a scaled version of a special instance of replicator dynamics. The latter also arises as the limiting differential equation for the empirical measures of a vertex reinforced random walk on a directed graph. We use this equivalence to show that for a class of positively $\alpha$-homogeneous rewards, $\alpha > 0$, the asymptotic outcome concentrates around the optimum in a certain limiting sense when `annealed' by letting $\alpha\uparrow\infty$ slowly. We also discuss connections with classical simulated annealing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge