Heavy-Tailed and Long-Range Dependent Noise in Stochastic Approximation: A Finite-Time Analysis

Stochastic approximation (SA) is a fundamental iterative framework with broad applications in reinforcement learning and optimization. Classical analyses typically rely on martingale difference or Markov noise with bounded second moments, but many practical settings, including finance and communications, frequently encounter heavy-tailed and long-range dependent (LRD) noise. In this work, we study SA for finding the root of a strongly monotone operator under these non-classical noise models. We establish the first finite-time moment bounds in both settings, providing explicit convergence rates that quantify the impact of heavy tails and temporal dependence. Our analysis employs a noise-averaging argument that regularizes the impact of noise without modifying the iteration. Finally, we apply our general framework to stochastic gradient descent (SGD) and gradient play, and corroborate our finite-time analysis through numerical experiments.

High-Probability Bounds for SGD under the Polyak-Lojasiewicz Condition with Markovian Noise

We present the first uniform-in-time high-probability bound for SGD under the PL condition, where the gradient noise contains both Markovian and martingale difference components. This significantly broadens the scope of finite-time guarantees, as the PL condition arises in many machine learning and deep learning models while Markovian noise naturally arises in decentralized optimization and online system identification problems. We further allow the magnitude of noise to grow with the function value, enabling the analysis of many practical sampling strategies. In addition to the high-probability guarantee, we establish a matching $1/k$ decay rate for the expected suboptimality. Our proof technique relies on the Poisson equation to handle the Markovian noise and a probabilistic induction argument to address the lack of almost-sure bounds on the objective. Finally, we demonstrate the applicability of our framework by analyzing three practical optimization problems: token-based decentralized linear regression, supervised learning with subsampling for privacy amplification, and online system identification.

Regret and Sample Complexity of Online Q-Learning via Concentration of Stochastic Approximation with Time-Inhomogeneous Markov Chains

We present the first high-probability regret bound for classical online Q-learning in infinite-horizon discounted Markov decision processes, without relying on optimism or bonus terms. We first analyze Boltzmann Q-learning with decaying temperature and show that its regret depends critically on the suboptimality gap of the MDP: for sufficiently large gaps, the regret is sublinear, while for small gaps it deteriorates and can approach linear growth. To address this limitation, we study a Smoothed $ε_n$-Greedy exploration scheme that combines $ε_n$-greedy and Boltzmann exploration, for which we prove a gap-robust regret bound of near-$\tilde{O}(N^{9/10})$. To analyze these algorithms, we develop a high-probability concentration bound for contractive Markovian stochastic approximation with iterate- and time-dependent transition dynamics. This bound may be of independent interest as the contraction factor in our bound is governed by the mixing time and is allowed to converge to one asymptotically.

$O(1/k)$ Finite-Time Bound for Non-Linear Two-Time-Scale Stochastic Approximation

Two-time-scale stochastic approximation is an algorithm with coupled iterations which has found broad applications in reinforcement learning, optimization and game control. While several prior works have obtained a mean square error bound of $O(1/k)$ for linear two-time-scale iterations, the best known bound in the non-linear contractive setting has been $O(1/k^{2/3})$. In this work, we obtain an improved bound of $O(1/k)$ for non-linear two-time-scale stochastic approximation. Our result applies to algorithms such as gradient descent-ascent and two-time-scale Lagrangian optimization. The key step in our analysis involves rewriting the original iteration in terms of an averaged noise sequence which decays sufficiently fast. Additionally, we use an induction-based approach to show that the iterates are bounded in expectation.

Non-Expansive Mappings in Two-Time-Scale Stochastic Approximation: Finite-Time Analysis

Two-time-scale stochastic approximation is an iterative algorithm used in applications such as optimization, reinforcement learning, and control. Finite-time analysis of these algorithms has primarily focused on fixed point iterations where both time-scales have contractive mappings. In this paper, we study two-time-scale iterations, where the slower time-scale has a non-expansive mapping. For such algorithms, the slower time-scale can be considered a stochastic inexact Krasnoselskii-Mann iteration. We show that the mean square error decays at a rate $O(1/k^{1/4-\epsilon})$, where $\epsilon>0$ is arbitrarily small. We also show almost sure convergence of iterates to the set of fixed points. We show the applicability of our framework by applying our results to minimax optimization, linear stochastic approximation, and Lagrangian optimization.

Learning to Control Unknown Strongly Monotone Games

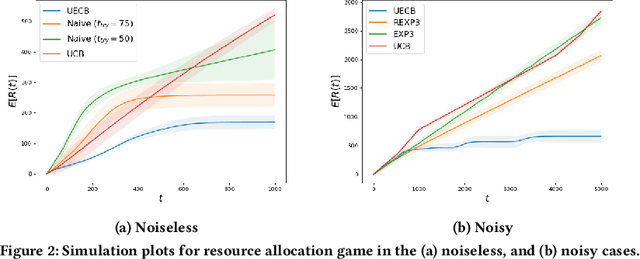
Consider $N$ players each with a $d$-dimensional action set. Each of the players' utility functions includes their reward function and a linear term for each dimension, with coefficients that are controlled by the manager. We assume that the game is strongly monotone, so if each player runs gradient descent, the dynamics converge to a unique Nash equilibrium (NE). The NE is typically inefficient in terms of global performance. The resulting global performance of the system can be improved by imposing $K$-dimensional linear constraints on the NE. We therefore want the manager to pick the controlled coefficients that impose the desired constraint on the NE. However, this requires knowing the players' reward functions and their action sets. Obtaining this game structure information is infeasible in a large-scale network and violates the users' privacy. To overcome this, we propose a simple algorithm that learns to shift the NE of the game to meet the linear constraints by adjusting the controlled coefficients online. Our algorithm only requires the linear constraints violation as feedback and does not need to know the reward functions or the action sets. We prove that our algorithm, which is based on two time-scale stochastic approximation, guarantees convergence with probability 1 to the set of NE that meet target linear constraints. We then provide a mean square convergence rate of $O(t^{-1/4})$ for our algorithm. This is the first such bound for two time-scale stochastic approximation where the slower time-scale is a fixed point iteration with a non-expansive mapping. We demonstrate how our scheme can be applied to optimizing a global quadratic cost at NE and load balancing in resource allocation games. We provide simulations of our algorithm for these scenarios.

A Concentration Bound for TD with Function Approximation

We derive a concentration bound of the type `for all $n \geq n_0$ for some $n_0$' for TD(0) with linear function approximation. We work with online TD learning with samples from a single sample path of the underlying Markov chain. This makes our analysis significantly different from offline TD learning or TD learning with access to independent samples from the stationary distribution of the Markov chain. We treat TD(0) as a contractive stochastic approximation algorithm, with both martingale and Markov noises. Markov noise is handled using the Poisson equation and the lack of almost sure guarantees on boundedness of iterates is handled using the concept of relaxed concentration inequalities.

Equilibrium Bandits: Learning Optimal Equilibria of Unknown Dynamics

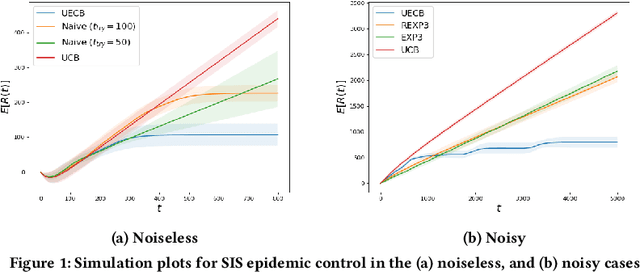
Consider a decision-maker that can pick one out of $K$ actions to control an unknown system, for $T$ turns. The actions are interpreted as different configurations or policies. Holding the same action fixed, the system asymptotically converges to a unique equilibrium, as a function of this action. The dynamics of the system are unknown to the decision-maker, which can only observe a noisy reward at the end of every turn. The decision-maker wants to maximize its accumulated reward over the $T$ turns. Learning what equilibria are better results in higher rewards, but waiting for the system to converge to equilibrium costs valuable time. Existing bandit algorithms, either stochastic or adversarial, achieve linear (trivial) regret for this problem. We present a novel algorithm, termed Upper Equilibrium Concentration Bound (UECB), that knows to switch an action quickly if it is not worth it to wait until the equilibrium is reached. This is enabled by employing convergence bounds to determine how far the system is from equilibrium. We prove that UECB achieves a regret of $\mathcal{O}(\log(T)+\tau_c\log(\tau_c)+\tau_c\log\log(T))$ for this equilibrium bandit problem where $\tau_c$ is the worst case approximate convergence time to equilibrium. We then show that both epidemic control and game control are special cases of equilibrium bandits, where $\tau_c\log \tau_c$ typically dominates the regret. We then test UECB numerically for both of these applications.

Reinforcement Learning in Non-Markovian Environments

Following the novel paradigm developed by Van Roy and coauthors for reinforcement learning in arbitrary non-Markovian environments, we propose a related formulation inspired by classical stochastic control that reduces the problem to recursive computation of approximate sufficient statistics.

A Concentration Bound for LSPE($λ$)

The popular LSPE($\lambda$) algorithm for policy evaluation is revisited to derive a concentration bound that gives high probability performance guarantees from some time on.