Learning to Control Unknown Strongly Monotone Games

Consider $N$ players each with a $d$-dimensional action set. Each of the players' utility functions includes their reward function and a linear term for each dimension, with coefficients that are controlled by the manager. We assume that the game is strongly monotone, so if each player runs gradient descent, the dynamics converge to a unique Nash equilibrium (NE). The NE is typically inefficient in terms of global performance. The resulting global performance of the system can be improved by imposing $K$-dimensional linear constraints on the NE. We therefore want the manager to pick the controlled coefficients that impose the desired constraint on the NE. However, this requires knowing the players' reward functions and their action sets. Obtaining this game structure information is infeasible in a large-scale network and violates the users' privacy. To overcome this, we propose a simple algorithm that learns to shift the NE of the game to meet the linear constraints by adjusting the controlled coefficients online. Our algorithm only requires the linear constraints violation as feedback and does not need to know the reward functions or the action sets. We prove that our algorithm, which is based on two time-scale stochastic approximation, guarantees convergence with probability 1 to the set of NE that meet target linear constraints. We then provide a mean square convergence rate of $O(t^{-1/4})$ for our algorithm. This is the first such bound for two time-scale stochastic approximation where the slower time-scale is a fixed point iteration with a non-expansive mapping. We demonstrate how our scheme can be applied to optimizing a global quadratic cost at NE and load balancing in resource allocation games. We provide simulations of our algorithm for these scenarios.

Equilibrium Bandits: Learning Optimal Equilibria of Unknown Dynamics

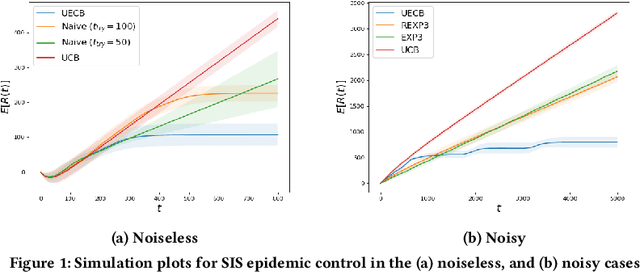
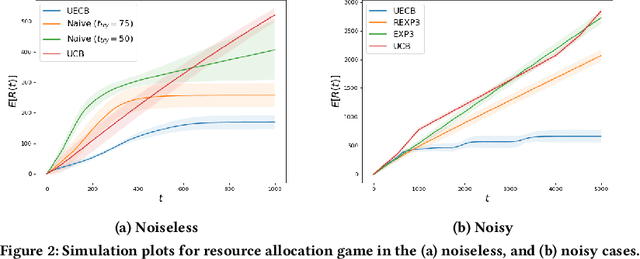
Consider a decision-maker that can pick one out of $K$ actions to control an unknown system, for $T$ turns. The actions are interpreted as different configurations or policies. Holding the same action fixed, the system asymptotically converges to a unique equilibrium, as a function of this action. The dynamics of the system are unknown to the decision-maker, which can only observe a noisy reward at the end of every turn. The decision-maker wants to maximize its accumulated reward over the $T$ turns. Learning what equilibria are better results in higher rewards, but waiting for the system to converge to equilibrium costs valuable time. Existing bandit algorithms, either stochastic or adversarial, achieve linear (trivial) regret for this problem. We present a novel algorithm, termed Upper Equilibrium Concentration Bound (UECB), that knows to switch an action quickly if it is not worth it to wait until the equilibrium is reached. This is enabled by employing convergence bounds to determine how far the system is from equilibrium. We prove that UECB achieves a regret of $\mathcal{O}(\log(T)+\tau_c\log(\tau_c)+\tau_c\log\log(T))$ for this equilibrium bandit problem where $\tau_c$ is the worst case approximate convergence time to equilibrium. We then show that both epidemic control and game control are special cases of equilibrium bandits, where $\tau_c\log \tau_c$ typically dominates the regret. We then test UECB numerically for both of these applications.

No Discounted-Regret Learning in Adversarial Bandits with Delays

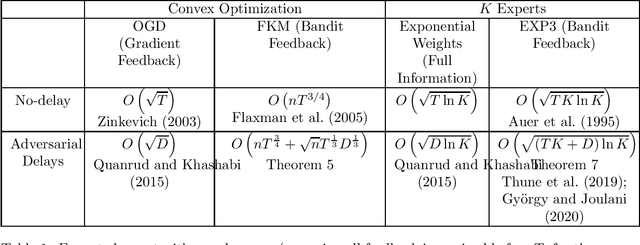
Consider a player that in each round $t$ out of $T$ rounds chooses an action and observes the incurred cost after a delay of $d_{t}$ rounds. The cost functions and the delay sequence are chosen by an adversary. We show that even if the players' algorithms lose their "no regret" property due to too large delays, the expected discounted ergodic distribution of play converges to the set of coarse correlated equilibrium (CCE) if the algorithms have "no discounted-regret". For a zero-sum game, we show that no discounted-regret is sufficient for the discounted ergodic average of play to converge to the set of Nash equilibria. We prove that the FKM algorithm with $n$ dimensions achieves a regret of $O\left(nT^{\frac{3}{4}}+\sqrt{n}T^{\frac{1}{3}}D^{\frac{1}{3}}\right)$ and the EXP3 algorithm with $K$ arms achieves a regret of $O\left(\sqrt{\ln K\left(KT+D\right)}\right)$ even when $D=\sum_{t=1}^{T}d_{t}$ and $T$ are unknown. These bounds use a novel doubling trick that provably retains the regret bound for when $D$ and $T$ are known. Using these bounds, we show that EXP3 and FKM have no discounted-regret even for $d_{t}=O\left(t\log t\right)$. Therefore, the CCE of a finite or convex unknown game can be approximated even when only delayed bandit feedback is available via simulation.

My Fair Bandit: Distributed Learning of Max-Min Fairness with Multi-player Bandits

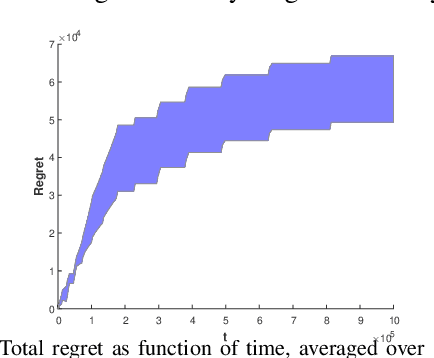
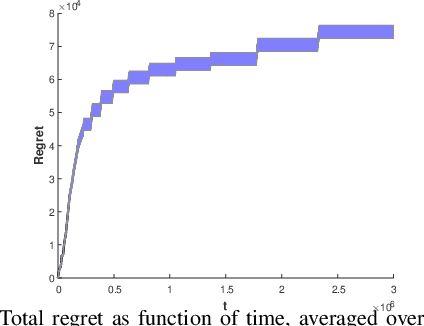
Consider N cooperative but non-communicating players where each plays one out of M arms for T turns. Players have different utilities for each arm, representable as an NxM matrix. These utilities are unknown to the players. In each turn players select an arm and receive a noisy observation of their utility for it. However, if any other players selected the same arm that turn, all colliding players will all receive zero utility due to the conflict. No other communication or coordination between the players is possible. Our goal is to design a distributed algorithm that learns the matching between players and arms that achieves max-min fairness while minimizing the regret. We present an algorithm and prove that it is regret optimal up to a $\log\log T$ factor. This is the first max-min fairness multi-player bandit algorithm with (near) order optimal regret.

Distributed Learning for Channel Allocation Over a Shared Spectrum

Channel allocation is the task of assigning channels to users such that some objective (e.g., sum-rate) is maximized. In centralized networks such as cellular networks, this task is carried by the base station which gathers the channel state information (CSI) from the users and computes the optimal solution. In distributed networks such as ad-hoc and device-to-device (D2D) networks, no base station exists and conveying global CSI between users is costly or simply impractical. When the CSI is time varying and unknown to the users, the users face the challenge of both learning the channel statistics online and converge to a good channel allocation. This introduces a multi-armed bandit (MAB) scenario with multiple decision makers. If two users or more choose the same channel, a collision occurs and they all receive zero reward. We propose a distributed channel allocation algorithm that each user runs and converges to the optimal allocation while achieving an order optimal regret of O\left(\log T\right). The algorithm is based on a carrier sensing multiple access (CSMA) implementation of the distributed auction algorithm. It does not require any exchange of information between users. Users need only to observe a single channel at a time and sense if there is a transmission on that channel, without decoding the transmissions or identifying the transmitting users. We demonstrate the performance of our algorithm using simulated LTE and 5G channels.