Approximate Probabilistic Inference for Time-Series Data A Robust Latent Gaussian Model With Temporal Awareness

The development of robust generative models for highly varied non-stationary time series data is a complex yet important problem. Traditional models for time series data prediction, such as Long Short-Term Memory (LSTM), are inefficient and generalize poorly as they cannot capture complex temporal relationships. In this paper, we present a probabilistic generative model that can be trained to capture temporal information, and that is robust to data errors. We call it Time Deep Latent Gaussian Model (tDLGM). Its novel architecture is inspired by Deep Latent Gaussian Model (DLGM). Our model is trained to minimize a loss function based on the negative log loss. One contributing factor to Time Deep Latent Gaussian Model (tDLGM) robustness is our regularizer, which accounts for data trends. Experiments conducted show that tDLGM is able to reconstruct and generate complex time series data, and that it is robust against to noise and faulty data.

Approximate Probabilistic Inference forTime-Series Data A Robust Latent Gaussian Model With Temporal Awareness

The development of robust generative models for highly varied non-stationary time series data is a complex yet important problem. Traditional models for time series data prediction, such as Long Short-Term Memory (LSTM), are inefficient and generalize poorly as they cannot capture complex temporal relationships. In this paper, we present a probabilistic generative model that can be trained to capture temporal information, and that is robust to data errors. We call it Time Deep Latent Gaussian Model (tDLGM). Its novel architecture is inspired by Deep Latent Gaussian Model (DLGM). Our model is trained to minimize a loss function based on the negative log loss. One contributing factor to Time Deep Latent Gaussian Model (tDLGM) robustness is our regularizer, which accounts for data trends. Experiments conducted show that tDLGM is able to reconstruct and generate complex time series data, and that it is robust against to noise and faulty data.

A Framework for Provably Stable and Consistent Training of Deep Feedforward Networks

We present a novel algorithm for training deep neural networks in supervised (classification and regression) and unsupervised (reinforcement learning) scenarios. This algorithm combines the standard stochastic gradient descent and the gradient clipping method. The output layer is updated using clipped gradients, the rest of the neural network is updated using standard gradients. Updating the output layer using clipped gradient stabilizes it. We show that the remaining layers are automatically stabilized provided the neural network is only composed of squashing (compact range) activations. We also present a novel squashing activation function - it is obtained by modifying a Gaussian Error Linear Unit (GELU) to have compact range - we call it Truncated GELU (tGELU). Unlike other squashing activations, such as sigmoid, the range of tGELU can be explicitly specified. As a consequence, the problem of vanishing gradients that arise due to a small range, e.g., in the case of a sigmoid activation, is eliminated. We prove that a NN composed of squashing activations (tGELU, sigmoid, etc.), when updated using the algorithm presented herein, is numerically stable and has consistent performance (low variance). The theory is supported by extensive experiments. Within reinforcement learning, as a consequence of our study, we show that target networks in Deep Q-Learning can be omitted, greatly speeding up learning and alleviating memory requirements. Cross-entropy based classification algorithms that suffer from high variance issues are more consistent when trained using our framework. One symptom of numerical instability in training is the high variance of the neural network update values. We show, in theory and through experiments, that our algorithm updates have low variance, and the training loss reduces in a smooth manner.

Stability and Convergence of Distributed Stochastic Approximations with large Unbounded Stochastic Information Delays

We generalize the Borkar-Meyn stability Theorem (BMT) to distributed stochastic approximations (SAs) with information delays that possess an arbitrary moment bound. To model the delays, we introduce Age of Information Processes (AoIPs): stochastic processes on the non-negative integers with a unit growth property. We show that AoIPs with an arbitrary moment bound cannot exceed any fraction of time infinitely often. In combination with a suitably chosen stepsize, this property turns out to be sufficient for the stability of distributed SAs. Compared to the BMT, our analysis requires crucial modifications and a new line of argument to handle the SA errors caused by AoI. In our analysis, we show that these SA errors satisfy a recursive inequality. To evaluate this recursion, we propose a new Gronwall-type inequality for time-varying lower limits of summations. As applications to our distributed BMT, we discuss distributed gradient-based optimization and a new approach to analyzing SAs with momentum.

Distributed gradient-based optimization in the presence of dependent aperiodic communication

Iterative distributed optimization algorithms involve multiple agents that communicate with each other, over time, in order to minimize/maximize a global objective. In the presence of unreliable communication networks, the Age-of-Information (AoI), which measures the freshness of data received, may be large and hence hinder algorithmic convergence. In this paper, we study the convergence of general distributed gradient-based optimization algorithms in the presence of communication that neither happens periodically nor at stochastically independent points in time. We show that convergence is guaranteed provided the random variables associated with the AoI processes are stochastically dominated by a random variable with finite first moment. This improves on previous requirements of boundedness of more than the first moment. We then introduce stochastically strongly connected (SSC) networks, a new stochastic form of strong connectedness for time-varying networks. We show: If for any $p \ge0$ the processes that describe the success of communication between agents in a SSC network are $\alpha$-mixing with $n^{p-1}\alpha(n)$ summable, then the associated AoI processes are stochastically dominated by a random variable with finite $p$-th moment. In combination with our first contribution, this implies that distributed stochastic gradient descend converges in the presence of AoI, if $\alpha(n)$ is summable.

Asymptotic Convergence of Deep Multi-Agent Actor-Critic Algorithms

We present sufficient conditions that ensure convergence of the multi-agent Deep Deterministic Policy Gradient (DDPG) algorithm. It is an example of one of the most popular paradigms of Deep Reinforcement Learning (DeepRL) for tackling continuous action spaces: the actor-critic paradigm. In the setting considered herein, each agent observes a part of the global state space in order to take local actions, for which it receives local rewards. For every agent, DDPG trains a local actor (policy) and a local critic (Q-function). The analysis shows that multi-agent DDPG using neural networks to approximate the local policies and critics converge to limits with the following properties: The critic limits minimize the average squared Bellman loss; the actor limits parameterize a policy that maximizes the local critic's approximation of $Q_i^*$, where $i$ is the agent index. The averaging is with respect to a probability distribution over the global state-action space. It captures the asymptotics of all local training processes. Finally, we extend the analysis to a fully decentralized setting where agents communicate over a wireless network prone to delays and losses; a typical scenario in, e.g., robotic applications.

Theory of Deep Q-Learning: A Dynamical Systems Perspective

Deep Q-Learning is an important algorithm, used to solve sequential decision making problems. It involves training a Deep Neural Network, called a Deep Q-Network (DQN), to approximate a function associated with optimal decision making, the Q-function. Although wildly successful in laboratory conditions, serious gaps between theory and practice prevent its use in the real-world. In this paper, we present a comprehensive analysis of the popular and practical version of the algorithm, under realistic verifiable assumptions. An important contribution is the characterization of its performance as a function of training. To do this, we view the algorithm as an evolving dynamical system. This facilitates associating a closely-related measure process with training. Then, the long-term behavior of Deep Q-Learning is determined by the limit of the aforementioned measure process. Empirical inferences, such as the qualitative advantage of using experience replay, and performance inconsistencies even after training, are explained using our analysis. Also, our theory is general and accommodates state Markov processes with multiple stationary distributions.

Deep reinforcement learning for scheduling in large-scale networked control systems

This work considers the problem of control and resource scheduling in networked systems. We present DIRA, a Deep reinforcement learning based Iterative Resource Allocation algorithm, which is scalable and control-aware. Our algorithm is tailored towards large-scale problems where control and scheduling need to act jointly to optimize performance. DIRA can be used to schedule general time-domain optimization based controllers. In the present work, we focus on control designs based on suitably adapted linear quadratic regulators. We apply our algorithm to networked systems with correlated fading communication channels. Our simulations show that DIRA scales well to large scheduling problems.

DSPG: Decentralized Simultaneous Perturbations Gradient Descent Scheme

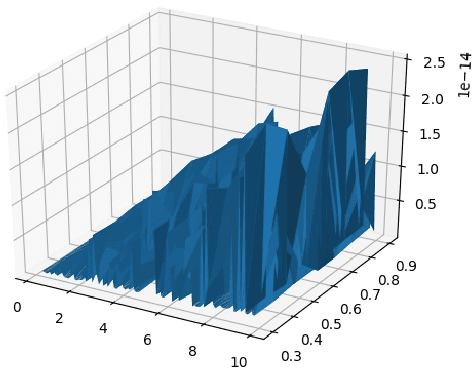
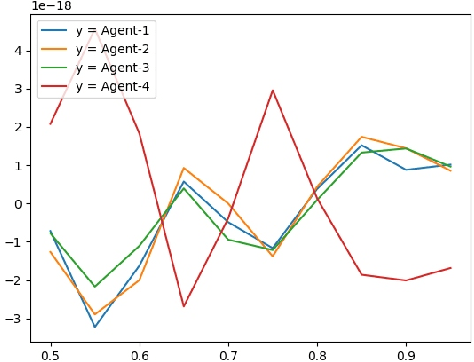
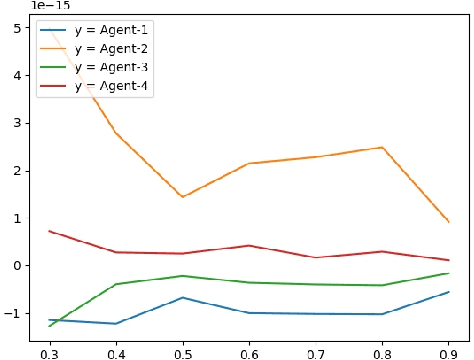
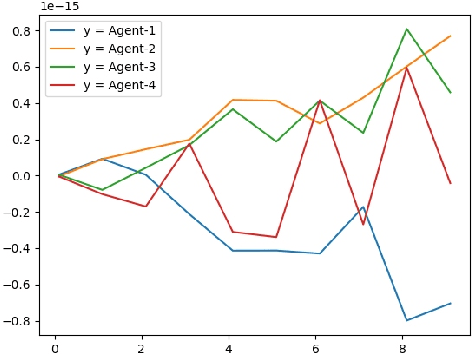
In this paper, we present an asynchronous approximate gradient method that is easy to implement called DSPG (Decentralized Simultaneous Perturbation Stochastic Approximations, with Constant Sensitivity Parameters). It is obtained by modifying SPSA (Simultaneous Perturbation Stochastic Approximations) to allow for decentralized optimization in multi-agent learning and distributed control scenarios. SPSA is a popular approximate gradient method developed by Spall, that is used in Robotics and Learning. In the multi-agent learning setup considered herein, the agents are assumed to be asynchronous (agents abide by their local clocks) and communicate via a wireless medium, that is prone to losses and delays. We analyze the gradient estimation bias that arises from setting the sensitivity parameters to a single value, and the bias that arises from communication losses and delays. Specifically, we show that these biases can be countered through better and frequent communication and/or by choosing a small fixed value for the sensitivity parameters. We also discuss the variance of the gradient estimator and its effect on the rate of convergence. Finally, we present numerical results supporting DSPG and the aforementioned theories and discussions.

Multi-Stage Reinforcement Learning For Object Detection

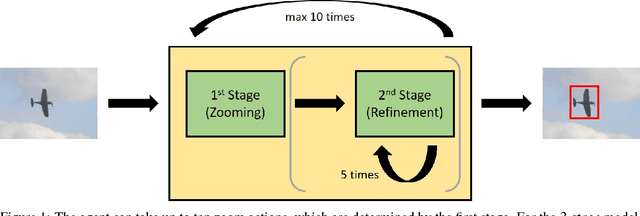
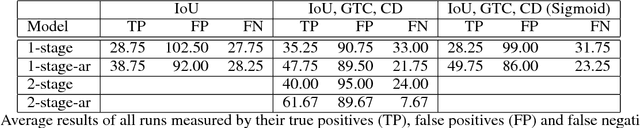
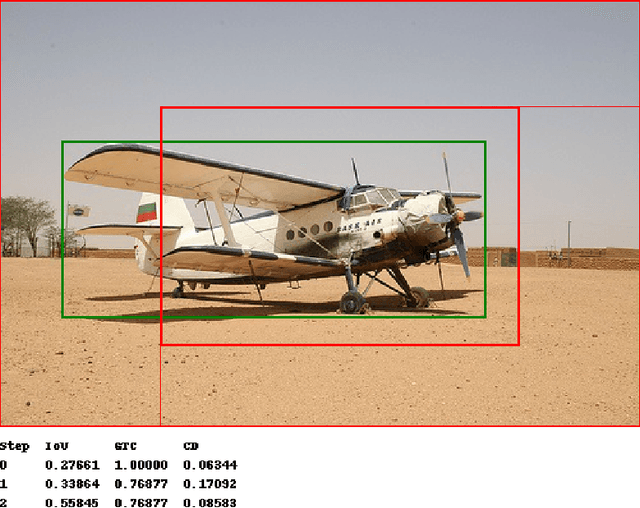
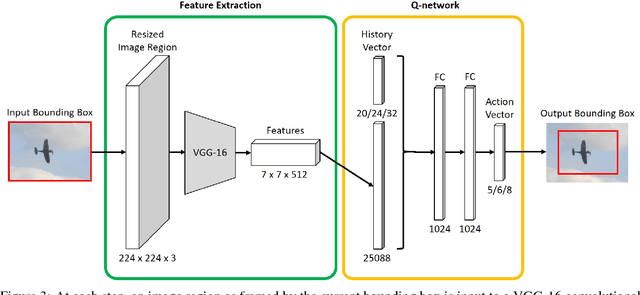
We present a reinforcement learning approach for detecting objects within an image. Our approach performs a step-wise deformation of a bounding box with the goal of tightly framing the object. It uses a hierarchical tree-like representation of predefined region candidates, which the agent can zoom in on. This reduces the number of region candidates that must be evaluated so that the agent can afford to compute new feature maps before each step to enhance detection quality. We compare an approach that is based purely on zoom actions with one that is extended by a second refinement stage to fine-tune the bounding box after each zoom step. We also improve the fitting ability by allowing for different aspect ratios of the bounding box. Finally, we propose different reward functions to lead to a better guidance of the agent while following its search trajectories. Experiments indicate that each of these extensions leads to more correct detections. The best performing approach comprises a zoom stage and a refinement stage, uses aspect-ratio modifying actions and is trained using a combination of three different reward metrics.