Approximate Probabilistic Inference for Time-Series Data A Robust Latent Gaussian Model With Temporal Awareness

The development of robust generative models for highly varied non-stationary time series data is a complex yet important problem. Traditional models for time series data prediction, such as Long Short-Term Memory (LSTM), are inefficient and generalize poorly as they cannot capture complex temporal relationships. In this paper, we present a probabilistic generative model that can be trained to capture temporal information, and that is robust to data errors. We call it Time Deep Latent Gaussian Model (tDLGM). Its novel architecture is inspired by Deep Latent Gaussian Model (DLGM). Our model is trained to minimize a loss function based on the negative log loss. One contributing factor to Time Deep Latent Gaussian Model (tDLGM) robustness is our regularizer, which accounts for data trends. Experiments conducted show that tDLGM is able to reconstruct and generate complex time series data, and that it is robust against to noise and faulty data.

Approximate Probabilistic Inference forTime-Series Data A Robust Latent Gaussian Model With Temporal Awareness

The development of robust generative models for highly varied non-stationary time series data is a complex yet important problem. Traditional models for time series data prediction, such as Long Short-Term Memory (LSTM), are inefficient and generalize poorly as they cannot capture complex temporal relationships. In this paper, we present a probabilistic generative model that can be trained to capture temporal information, and that is robust to data errors. We call it Time Deep Latent Gaussian Model (tDLGM). Its novel architecture is inspired by Deep Latent Gaussian Model (DLGM). Our model is trained to minimize a loss function based on the negative log loss. One contributing factor to Time Deep Latent Gaussian Model (tDLGM) robustness is our regularizer, which accounts for data trends. Experiments conducted show that tDLGM is able to reconstruct and generate complex time series data, and that it is robust against to noise and faulty data.

Exact Spectral Norm Regularization for Neural Networks

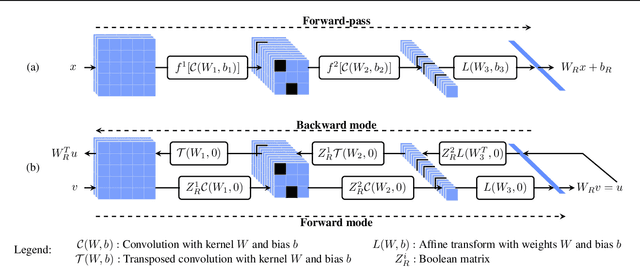
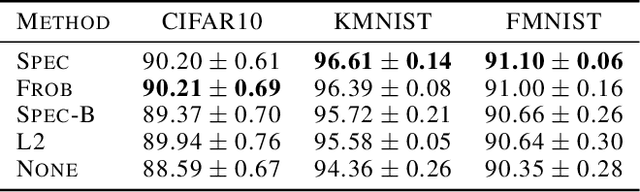
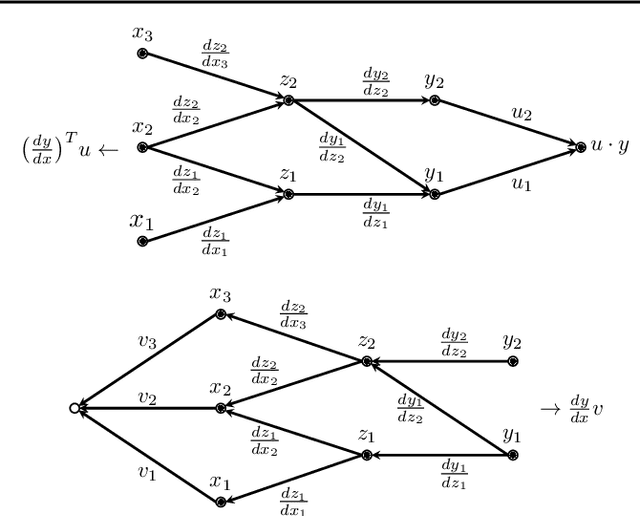
We pursue a line of research that seeks to regularize the spectral norm of the Jacobian of the input-output mapping for deep neural networks. While previous work rely on upper bounding techniques, we provide a scheme that targets the exact spectral norm. We showcase that our algorithm achieves an improved generalization performance compared to previous spectral regularization techniques while simultaneously maintaining a strong safeguard against natural and adversarial noise. Moreover, we further explore some previous reasoning concerning the strong adversarial protection that Jacobian regularization provides and show that it can be misleading.

SilGAN: Generating driving maneuvers for scenario-based software-in-the-loop testing

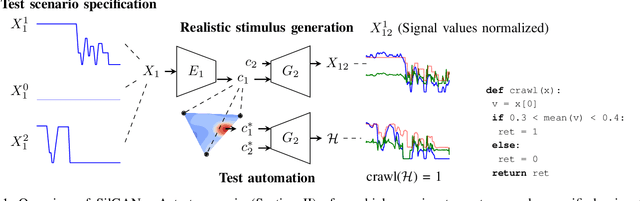
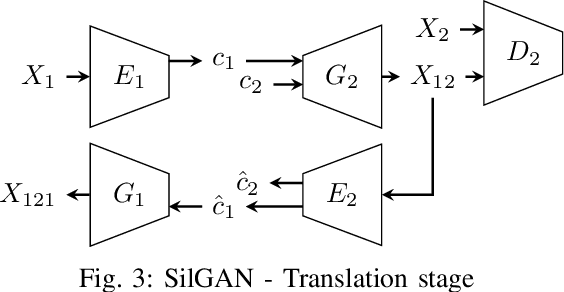
Automotive software testing continues to rely largely upon expensive field tests to ensure quality because alternatives like simulation-based testing are relatively immature. As a step towards lowering reliance on field tests, we present SilGAN, a deep generative model that eases specification, stimulus generation, and automation of automotive software-in-the-loop testing. The model is trained using data recorded from vehicles in the field. Upon training, the model uses a concise specification for a driving scenario to generate realistic vehicle state transitions that can occur during such a scenario. Such authentic emulation of internal vehicle behavior can be used for rapid, systematic and inexpensive testing of vehicle control software. In addition, by presenting a targeted method for searching through the information learned by the model, we show how a test objective like code coverage can be automated. The data driven end-to-end testing pipeline that we present vastly expands the scope and credibility of automotive simulation-based testing. This reduces time to market while helping maintain required standards of quality.

Slope and generalization properties of neural networks

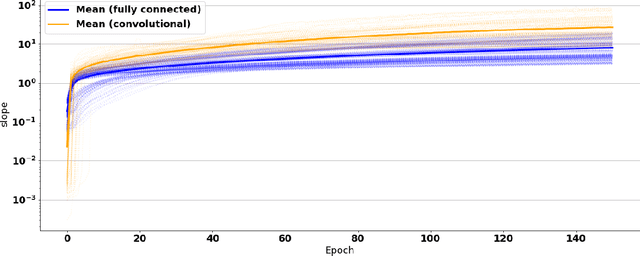
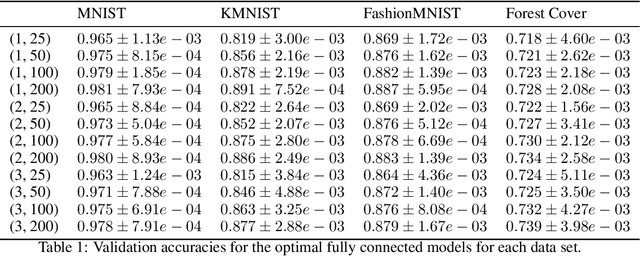
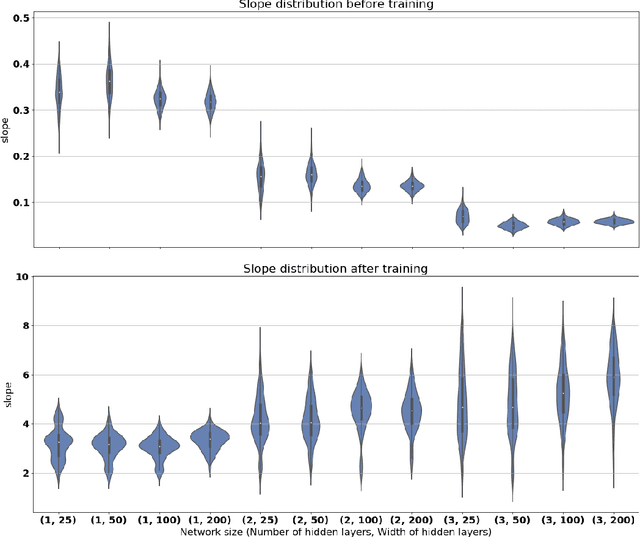
Neural networks are very successful tools in for example advanced classification. From a statistical point of view, fitting a neural network may be seen as a kind of regression, where we seek a function from the input space to a space of classification probabilities that follows the "general" shape of the data, but avoids overfitting by avoiding memorization of individual data points. In statistics, this can be done by controlling the geometric complexity of the regression function. We propose to do something similar when fitting neural networks by controlling the slope of the network. After defining the slope and discussing some of its theoretical properties, we go on to show empirically in examples, using ReLU networks, that the distribution of the slope of a well-trained neural network classifier is generally independent of the width of the layers in a fully connected network, and that the mean of the distribution only has a weak dependence on the model architecture in general. The slope is of similar size throughout the relevant volume, and varies smoothly. It also behaves as predicted in rescaling examples. We discuss possible applications of the slope concept, such as using it as a part of the loss function or stopping criterion during network training, or ranking data sets in terms of their complexity.

Does the dataset meet your expectations? Explaining sample representation in image data

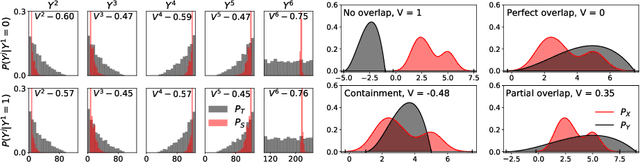
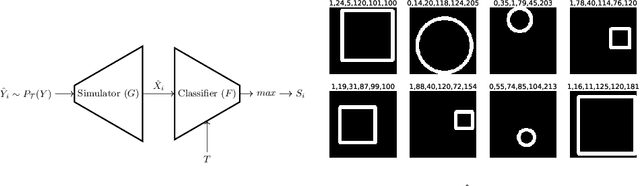
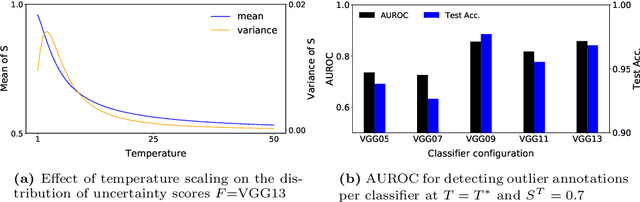
Since the behavior of a neural network model is adversely affected by a lack of diversity in training data, we present a method that identifies and explains such deficiencies. When a dataset is labeled, we note that annotations alone are capable of providing a human interpretable summary of sample diversity. This allows explaining any lack of diversity as the mismatch found when comparing the \textit{actual} distribution of annotations in the dataset with an \textit{expected} distribution of annotations, specified manually to capture essential label diversity. While, in many practical cases, labeling (samples $\rightarrow$ annotations) is expensive, its inverse, simulation (annotations $\rightarrow$ samples) can be cheaper. By mapping the expected distribution of annotations into test samples using parametric simulation, we present a method that explains sample representation using the mismatch in diversity between simulated and collected data. We then apply the method to examine a dataset of geometric shapes to qualitatively and quantitatively explain sample representation in terms of comprehensible aspects such as size, position, and pixel brightness.