Exact Spectral Norm Regularization for Neural Networks

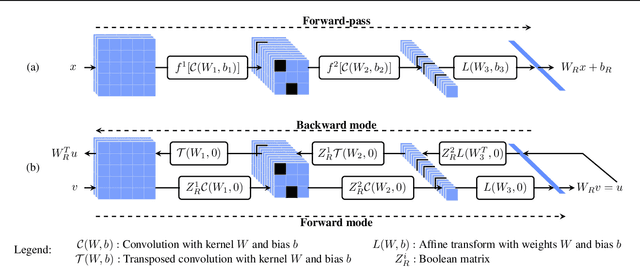
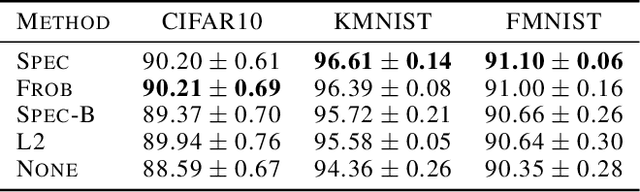
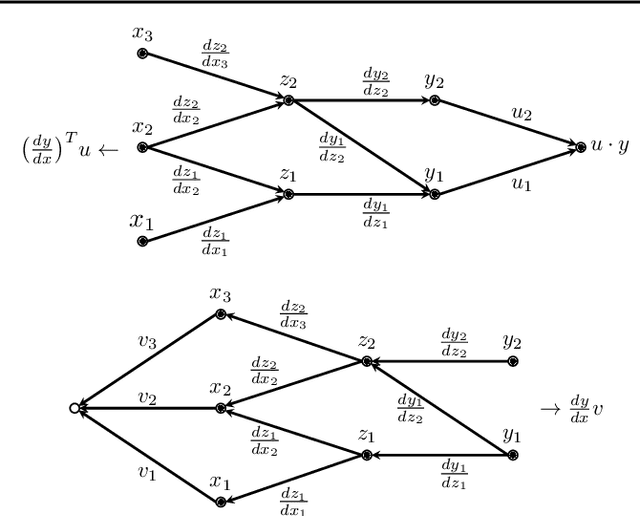
We pursue a line of research that seeks to regularize the spectral norm of the Jacobian of the input-output mapping for deep neural networks. While previous work rely on upper bounding techniques, we provide a scheme that targets the exact spectral norm. We showcase that our algorithm achieves an improved generalization performance compared to previous spectral regularization techniques while simultaneously maintaining a strong safeguard against natural and adversarial noise. Moreover, we further explore some previous reasoning concerning the strong adversarial protection that Jacobian regularization provides and show that it can be misleading.

Slope and generalization properties of neural networks

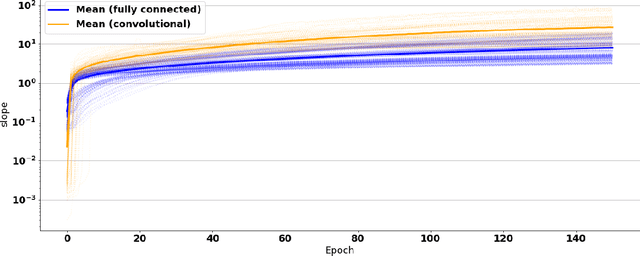
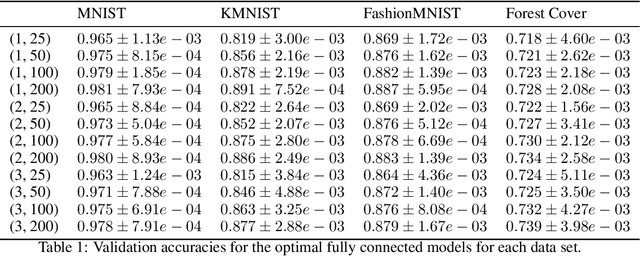
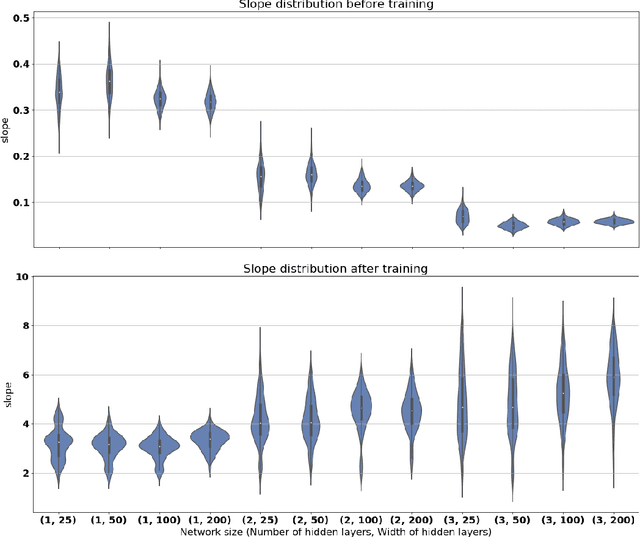
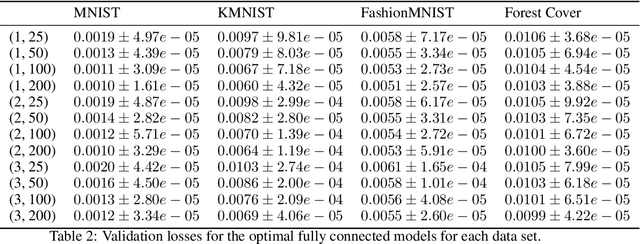
Neural networks are very successful tools in for example advanced classification. From a statistical point of view, fitting a neural network may be seen as a kind of regression, where we seek a function from the input space to a space of classification probabilities that follows the "general" shape of the data, but avoids overfitting by avoiding memorization of individual data points. In statistics, this can be done by controlling the geometric complexity of the regression function. We propose to do something similar when fitting neural networks by controlling the slope of the network. After defining the slope and discussing some of its theoretical properties, we go on to show empirically in examples, using ReLU networks, that the distribution of the slope of a well-trained neural network classifier is generally independent of the width of the layers in a fully connected network, and that the mean of the distribution only has a weak dependence on the model architecture in general. The slope is of similar size throughout the relevant volume, and varies smoothly. It also behaves as predicted in rescaling examples. We discuss possible applications of the slope concept, such as using it as a part of the loss function or stopping criterion during network training, or ranking data sets in terms of their complexity.