Exact Spectral Norm Regularization for Neural Networks
Paper and Code
Jun 27, 2022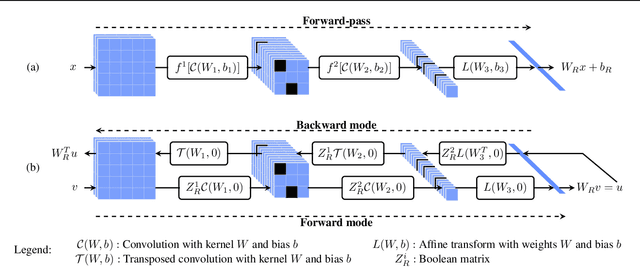
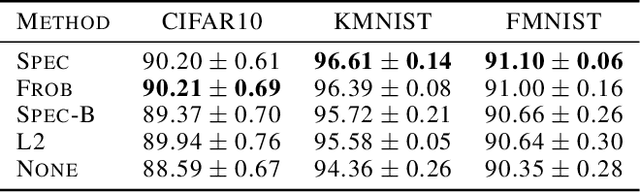
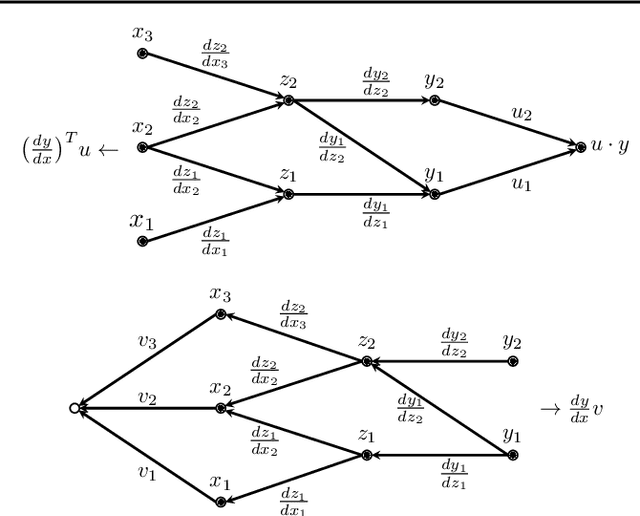

We pursue a line of research that seeks to regularize the spectral norm of the Jacobian of the input-output mapping for deep neural networks. While previous work rely on upper bounding techniques, we provide a scheme that targets the exact spectral norm. We showcase that our algorithm achieves an improved generalization performance compared to previous spectral regularization techniques while simultaneously maintaining a strong safeguard against natural and adversarial noise. Moreover, we further explore some previous reasoning concerning the strong adversarial protection that Jacobian regularization provides and show that it can be misleading.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge