Approximate Linear Programming and Decentralized Policy Improvement in Cooperative Multi-agent Markov Decision Processes

In this work, we consider a `cooperative' multi-agent Markov decision process (MDP) involving m greater than 1 agents, where all agents are aware of the system model. At each decision epoch, all the m agents cooperatively select actions in order to maximize a common long-term objective. Since the number of actions grows exponentially in the number of agents, policy improvement is computationally expensive. Recent works have proposed using decentralized policy improvement in which each agent assumes that the decisions of the other agents are fixed and it improves its decisions unilaterally. Yet, in these works, exact values are computed. In our work, for cooperative multi-agent finite and infinite horizon discounted MDPs, we propose suitable approximate policy iteration algorithms, wherein we use approximate linear programming to compute the approximate value function and use decentralized policy improvement. Thus our algorithms can handle both large number of states as well as multiple agents. We provide theoretical guarantees for our algorithms and also demonstrate the performance of our algorithms on some numerical examples.

n-Step Temporal Difference Learning with Optimal n

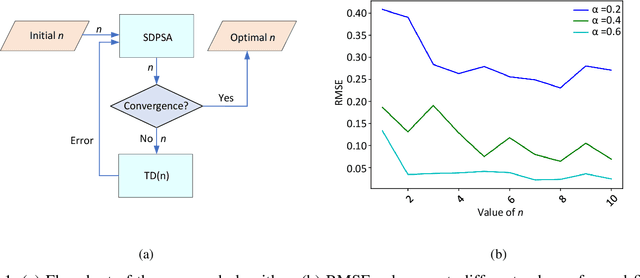
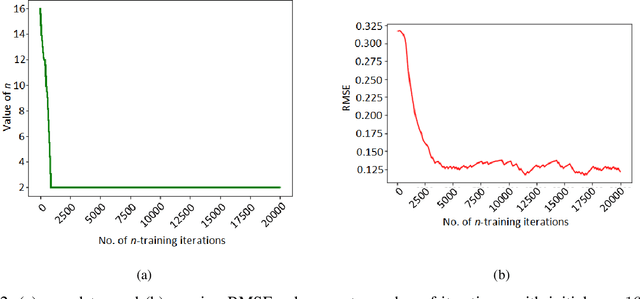
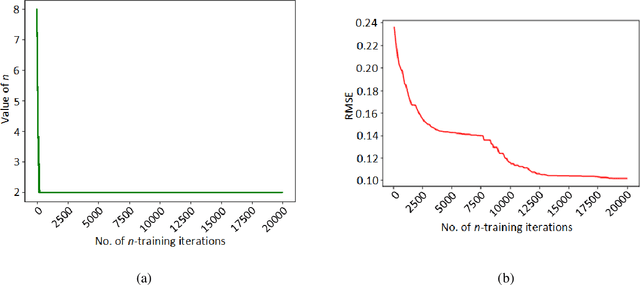
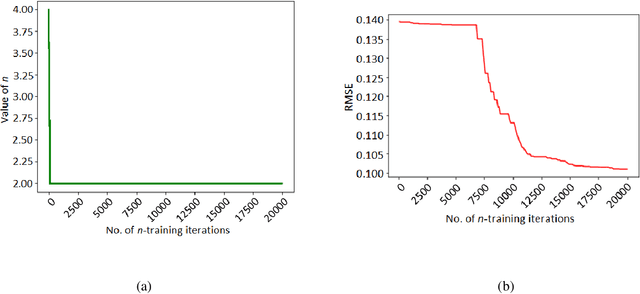
We consider the problem of finding the optimal value of n in the n-step temporal difference (TD) algorithm. We find the optimal n by resorting to the model-free optimization technique of simultaneous perturbation stochastic approximation (SPSA). We adopt a one-simulation SPSA procedure that is originally for continuous optimization to the discrete optimization framework but incorporates a cyclic perturbation sequence. We prove the convergence of our proposed algorithm, SDPSA, and show that it finds the optimal value of n in n-step TD. Through experiments, we show that the optimal value of n is achieved with SDPSA for any arbitrary initial value of the same.