Weighted bandits or: How bandits learn distorted values that are not expected

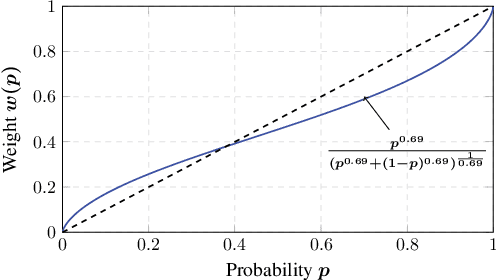
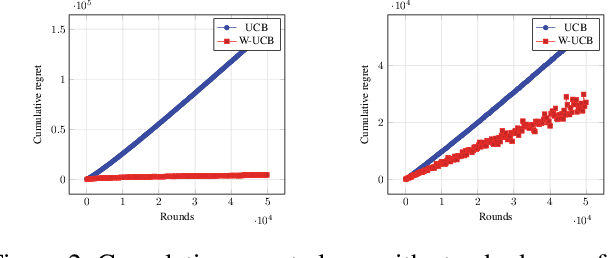
Motivated by models of human decision making proposed to explain commonly observed deviations from conventional expected value preferences, we formulate two stochastic multi-armed bandit problems with distorted probabilities on the cost distributions: the classic $K$-armed bandit and the linearly parameterized bandit. In both settings, we propose algorithms that are inspired by Upper Confidence Bound (UCB), incorporate cost distortions, and exhibit sublinear regret assuming \holder continuous weight distortion functions. For the $K$-armed setting, we show that the algorithm, called W-UCB, achieves problem-dependent regret $O(L^2 M^2 \log n/ \Delta^{\frac{2}{\alpha}-1})$, where $n$ is the number of plays, $\Delta$ is the gap in distorted expected value between the best and next best arm, $L$ and $\alpha$ are the H\"{o}lder constants for the distortion function, and $M$ is an upper bound on costs, and a problem-independent regret bound of $O((KL^2M^2)^{\alpha/2}n^{(2-\alpha)/2})$. We also present a matching lower bound on the regret, showing that the regret of W-UCB is essentially unimprovable over the class of H\"{o}lder-continuous weight distortions. For the linearly parameterized setting, we develop a new algorithm, a variant of the Optimism in the Face of Uncertainty Linear bandit (OFUL) algorithm called WOFUL (Weight-distorted OFUL), and show that it has regret $O(d\sqrt{n} \; \mbox{polylog}(n))$ with high probability, for sub-Gaussian cost distributions. Finally, numerical examples demonstrate the advantages resulting from using distortion-aware learning algorithms.

Cumulative Prospect Theory Meets Reinforcement Learning: Prediction and Control

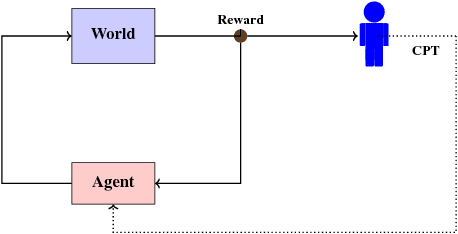
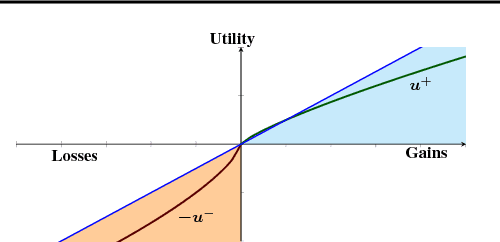
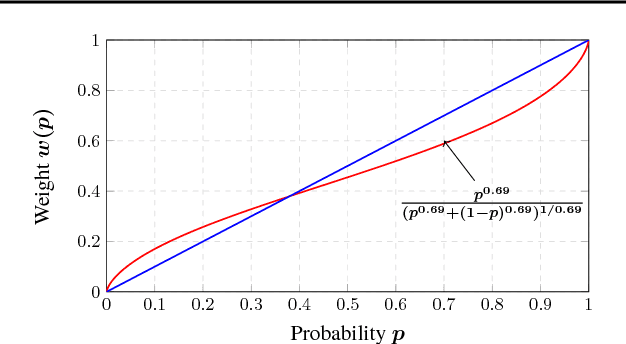
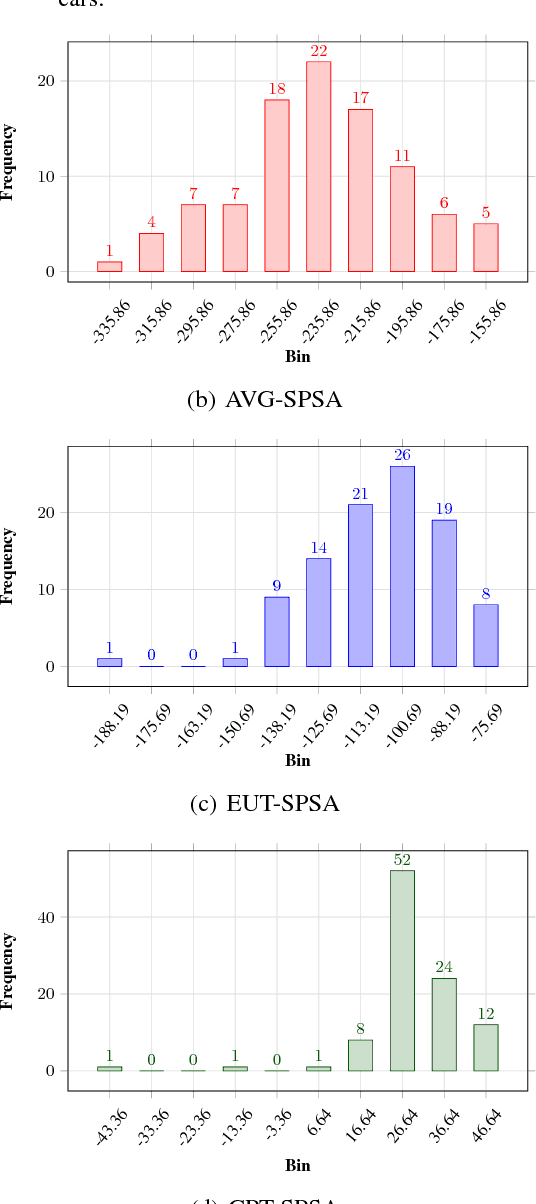
Cumulative prospect theory (CPT) is known to model human decisions well, with substantial empirical evidence supporting this claim. CPT works by distorting probabilities and is more general than the classic expected utility and coherent risk measures. We bring this idea to a risk-sensitive reinforcement learning (RL) setting and design algorithms for both estimation and control. The RL setting presents two particular challenges when CPT is applied: estimating the CPT objective requires estimations of the entire distribution of the value function and finding a randomized optimal policy. The estimation scheme that we propose uses the empirical distribution to estimate the CPT-value of a random variable. We then use this scheme in the inner loop of a CPT-value optimization procedure that is based on the well-known simulation optimization idea of simultaneous perturbation stochastic approximation (SPSA). We provide theoretical convergence guarantees for all the proposed algorithms and also illustrate the usefulness of CPT-based criteria in a traffic signal control application.

Adaptive system optimization using random directions stochastic approximation

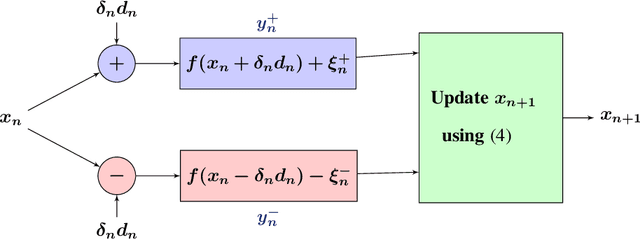
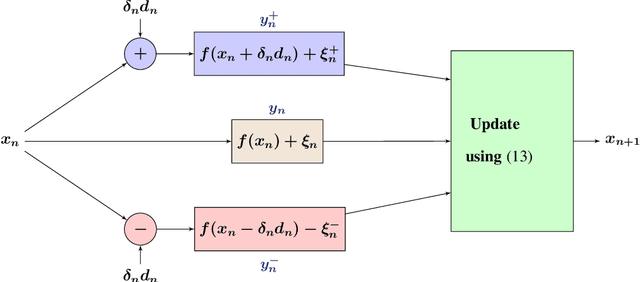
We present novel algorithms for simulation optimization using random directions stochastic approximation (RDSA). These include first-order (gradient) as well as second-order (Newton) schemes. We incorporate both continuous-valued as well as discrete-valued perturbations into both our algorithms. The former are chosen to be independent and identically distributed (i.i.d.) symmetric, uniformly distributed random variables (r.v.), while the latter are i.i.d., asymmetric, Bernoulli r.v.s. Our Newton algorithm, with a novel Hessian estimation scheme, requires N-dimensional perturbations and three loss measurements per iteration, whereas the simultaneous perturbation Newton search algorithm of [1] requires 2N-dimensional perturbations and four loss measurements per iteration. We prove the unbiasedness of both gradient and Hessian estimates and asymptotic (strong) convergence for both first-order and second-order schemes. We also provide asymptotic normality results, which in particular establish that the asymmetric Bernoulli variant of Newton RDSA method is better than 2SPSA of [1]. Numerical experiments are used to validate the theoretical results.