Stochastic approximation for speeding up LSTD (and LSPI)

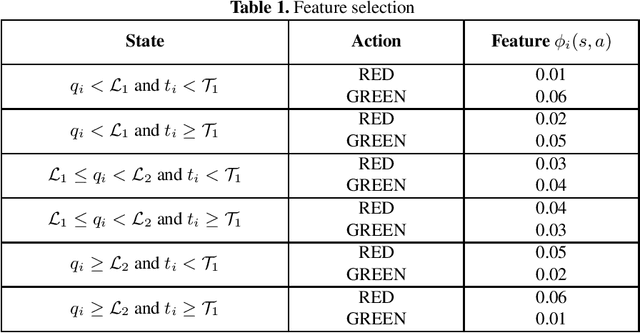
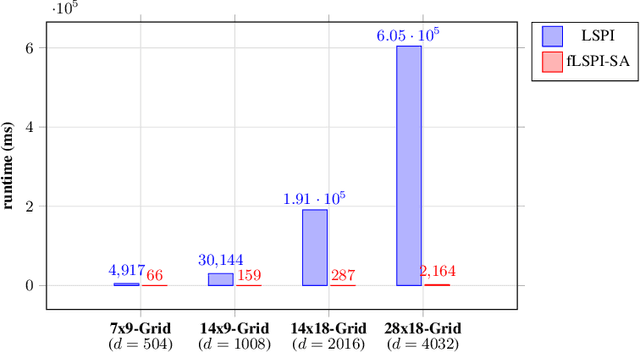
We propose a stochastic approximation (SA) based method with randomization of samples for policy evaluation using the least squares temporal difference (LSTD) algorithm. Our method results in an $O(d)$ improvement in complexity in comparison to regular LSTD, where $d$ is the dimension of the data. We provide convergence rate results for our proposed method, both in high probability and in expectation. Moreover, we also establish that using our scheme in place of LSTD does not impact the rate of convergence of the approximate value function to the true value function and hence a low-complexity LSPI variant that uses our SA based scheme has the same order of the performance bounds as that of regular LSPI. These rate results coupled with the low complexity of our method make it attractive for implementation in big data settings, where $d$ is large. Furthermore, we analyze a similar low-complexity alternative for least squares regression and provide finite-time bounds there. We demonstrate the practicality of our method for LSTD empirically by combining it with the LSPI algorithm in a traffic signal control application. We also conduct another set of experiments that combines the SA based low-complexity variant for least squares regression with the LinUCB algorithm for contextual bandits, using the large scale news recommendation dataset from Yahoo.

On TD(0) with function approximation: Concentration bounds and a centered variant with exponential convergence

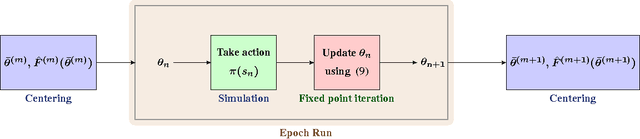
We provide non-asymptotic bounds for the well-known temporal difference learning algorithm TD(0) with linear function approximators. These include high-probability bounds as well as bounds in expectation. Our analysis suggests that a step-size inversely proportional to the number of iterations cannot guarantee optimal rate of convergence unless we assume (partial) knowledge of the stationary distribution for the Markov chain underlying the policy considered. We also provide bounds for the iterate averaged TD(0) variant, which gets rid of the step-size dependency while exhibiting the optimal rate of convergence. Furthermore, we propose a variant of TD(0) with linear approximators that incorporates a centering sequence, and establish that it exhibits an exponential rate of convergence in expectation. We demonstrate the usefulness of our bounds on two synthetic experimental settings.

Fast gradient descent for drifting least squares regression, with application to bandits

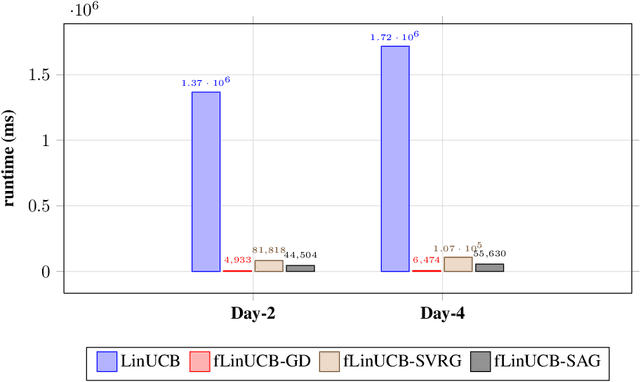
Online learning algorithms require to often recompute least squares regression estimates of parameters. We study improving the computational complexity of such algorithms by using stochastic gradient descent (SGD) type schemes in place of classic regression solvers. We show that SGD schemes efficiently track the true solutions of the regression problems, even in the presence of a drift. This finding coupled with an $O(d)$ improvement in complexity, where $d$ is the dimension of the data, make them attractive for implementation in the big data settings. In the case when strong convexity in the regression problem is guaranteed, we provide bounds on the error both in expectation and high probability (the latter is often needed to provide theoretical guarantees for higher level algorithms), despite the drifting least squares solution. As an example of this case we prove that the regret performance of an SGD version of the PEGE linear bandit algorithm [Rusmevichientong and Tsitsiklis 2010] is worse that that of PEGE itself only by a factor of $O(\log^4 n)$. When strong convexity of the regression problem cannot be guaranteed, we investigate using an adaptive regularisation. We make an empirical study of an adaptively regularised, SGD version of LinUCB [Li et al. 2010] in a news article recommendation application, which uses the large scale news recommendation dataset from Yahoo! front page. These experiments show a large gain in computational complexity, with a consistently low tracking error and click-through-rate (CTR) performance that is $75\%$ close.

Finite-Time Analysis of Kernelised Contextual Bandits

We tackle the problem of online reward maximisation over a large finite set of actions described by their contexts. We focus on the case when the number of actions is too big to sample all of them even once. However we assume that we have access to the similarities between actions' contexts and that the expected reward is an arbitrary linear function of the contexts' images in the related reproducing kernel Hilbert space (RKHS). We propose KernelUCB, a kernelised UCB algorithm, and give a cumulative regret bound through a frequentist analysis. For contextual bandits, the related algorithm GP-UCB turns out to be a special case of our algorithm, and our finite-time analysis improves the regret bound of GP-UCB for the agnostic case, both in the terms of the kernel-dependent quantity and the RKHS norm of the reward function. Moreover, for the linear kernel, our regret bound matches the lower bound for contextual linear bandits.

Thompson Sampling for 1-Dimensional Exponential Family Bandits

Thompson Sampling has been demonstrated in many complex bandit models, however the theoretical guarantees available for the parametric multi-armed bandit are still limited to the Bernoulli case. Here we extend them by proving asymptotic optimality of the algorithm using the Jeffreys prior for 1-dimensional exponential family bandits. Our proof builds on previous work, but also makes extensive use of closed forms for Kullback-Leibler divergence and Fisher information (and thus Jeffreys prior) available in an exponential family. This allow us to give a finite time exponential concentration inequality for posterior distributions on exponential families that may be of interest in its own right. Moreover our analysis covers some distributions for which no optimistic algorithm has yet been proposed, including heavy-tailed exponential families.

Thompson Sampling: An Asymptotically Optimal Finite Time Analysis

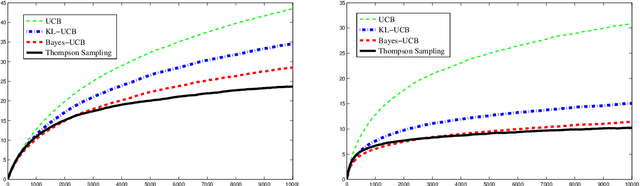
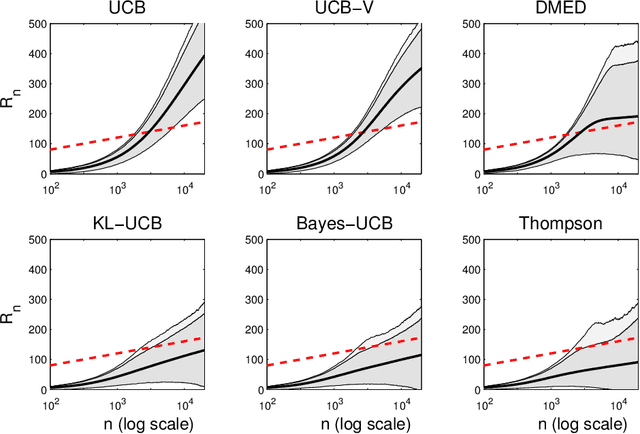
The question of the optimality of Thompson Sampling for solving the stochastic multi-armed bandit problem had been open since 1933. In this paper we answer it positively for the case of Bernoulli rewards by providing the first finite-time analysis that matches the asymptotic rate given in the Lai and Robbins lower bound for the cumulative regret. The proof is accompanied by a numerical comparison with other optimal policies, experiments that have been lacking in the literature until now for the Bernoulli case.