On overfitting and asymptotic bias in batch reinforcement learning with partial observability

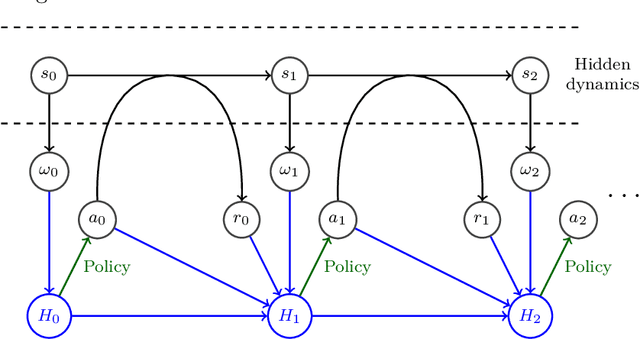
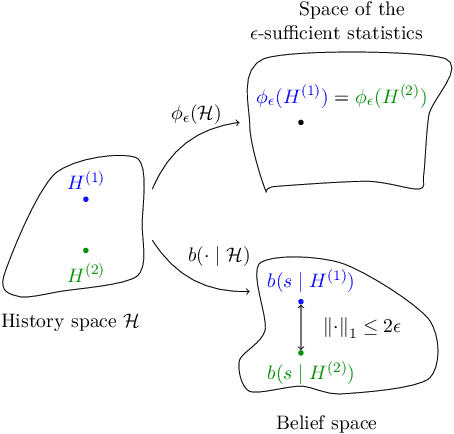
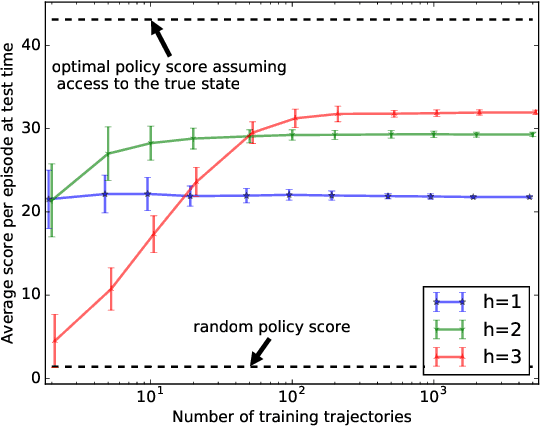
This paper stands in the context of reinforcement learning with partial observability and limited data. In this setting, we focus on the tradeoff between asymptotic bias (suboptimality with unlimited data) and overfitting (additional suboptimality due to limited data), and theoretically show that while potentially increasing the asymptotic bias, a smaller state representation decreases the risk of overfitting. Our analysis relies on expressing the quality of a state representation by bounding L1 error terms of the associated belief states. Theoretical results are empirically illustrated when the state representation is a truncated history of observations. Finally, we also discuss and empirically illustrate how using function approximators and adapting the discount factor may enhance the tradeoff between asymptotic bias and overfitting.

How to Discount Deep Reinforcement Learning: Towards New Dynamic Strategies

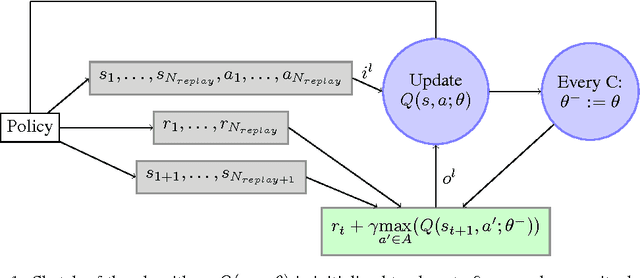
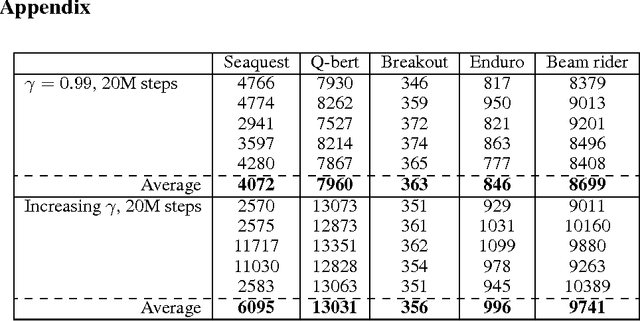
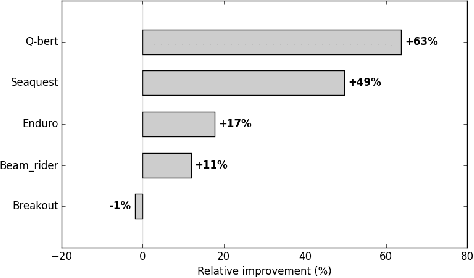
Using deep neural nets as function approximator for reinforcement learning tasks have recently been shown to be very powerful for solving problems approaching real-world complexity. Using these results as a benchmark, we discuss the role that the discount factor may play in the quality of the learning process of a deep Q-network (DQN). When the discount factor progressively increases up to its final value, we empirically show that it is possible to significantly reduce the number of learning steps. When used in conjunction with a varying learning rate, we empirically show that it outperforms original DQN on several experiments. We relate this phenomenon with the instabilities of neural networks when they are used in an approximate Dynamic Programming setting. We also describe the possibility to fall within a local optimum during the learning process, thus connecting our discussion with the exploration/exploitation dilemma.

Benchmarking for Bayesian Reinforcement Learning

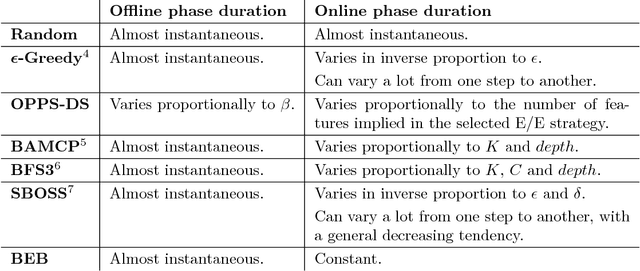
In the Bayesian Reinforcement Learning (BRL) setting, agents try to maximise the collected rewards while interacting with their environment while using some prior knowledge that is accessed beforehand. Many BRL algorithms have already been proposed, but even though a few toy examples exist in the literature, there are still no extensive or rigorous benchmarks to compare them. The paper addresses this problem, and provides a new BRL comparison methodology along with the corresponding open source library. In this methodology, a comparison criterion that measures the performance of algorithms on large sets of Markov Decision Processes (MDPs) drawn from some probability distributions is defined. In order to enable the comparison of non-anytime algorithms, our methodology also includes a detailed analysis of the computation time requirement of each algorithm. Our library is released with all source code and documentation: it includes three test problems, each of which has two different prior distributions, and seven state-of-the-art RL algorithms. Finally, our library is illustrated by comparing all the available algorithms and the results are discussed.

Simultaneous Perturbation Algorithms for Batch Off-Policy Search

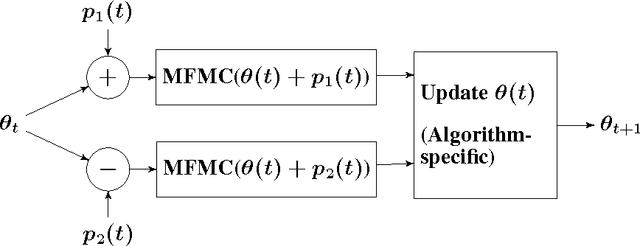
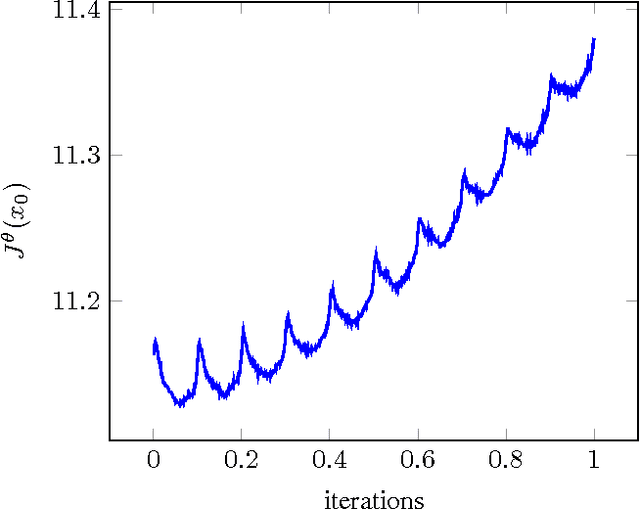
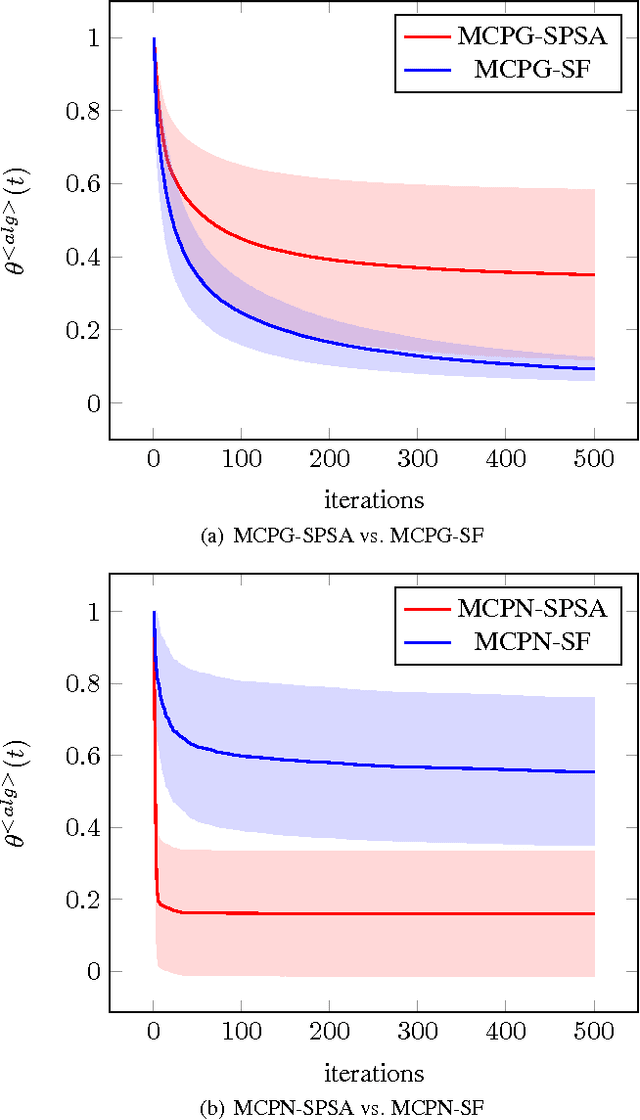
We propose novel policy search algorithms in the context of off-policy, batch mode reinforcement learning (RL) with continuous state and action spaces. Given a batch collection of trajectories, we perform off-line policy evaluation using an algorithm similar to that by [Fonteneau et al., 2010]. Using this Monte-Carlo like policy evaluator, we perform policy search in a class of parameterized policies. We propose both first order policy gradient and second order policy Newton algorithms. All our algorithms incorporate simultaneous perturbation estimates for the gradient as well as the Hessian of the cost-to-go vector, since the latter is unknown and only biased estimates are available. We demonstrate their practicality on a simple 1-dimensional continuous state space problem.

Min Max Generalization for Two-stage Deterministic Batch Mode Reinforcement Learning: Relaxation Schemes

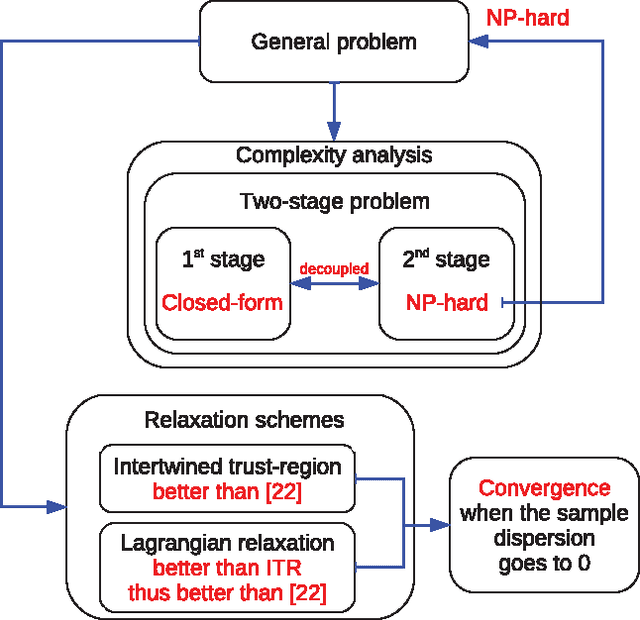
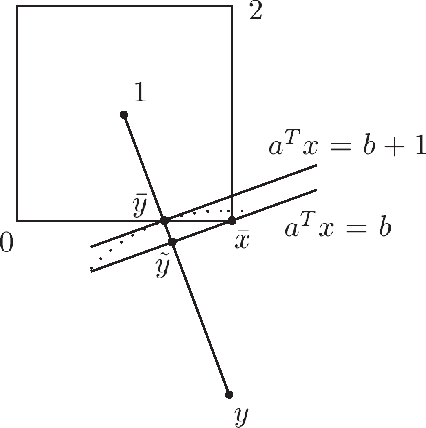
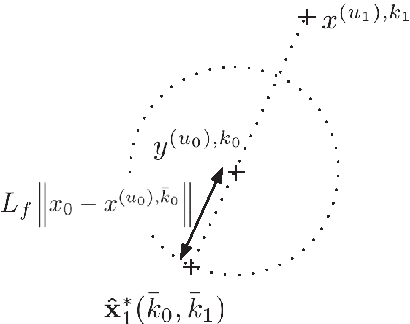
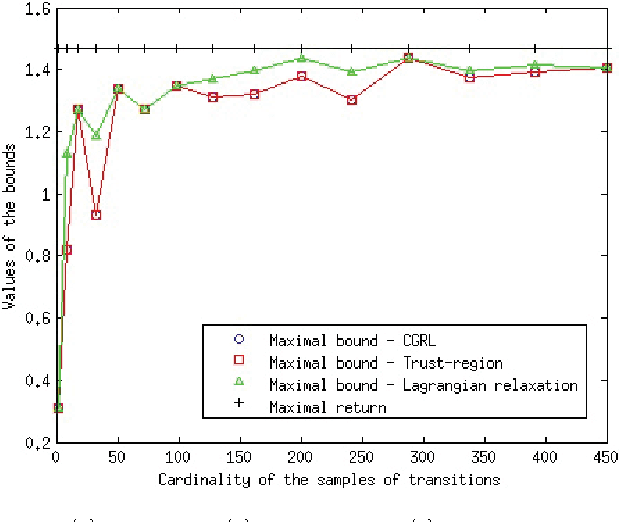
We study the minmax optimization problem introduced in [22] for computing policies for batch mode reinforcement learning in a deterministic setting. First, we show that this problem is NP-hard. In the two-stage case, we provide two relaxation schemes. The first relaxation scheme works by dropping some constraints in order to obtain a problem that is solvable in polynomial time. The second relaxation scheme, based on a Lagrangian relaxation where all constraints are dualized, leads to a conic quadratic programming problem. We also theoretically prove and empirically illustrate that both relaxation schemes provide better results than those given in [22].