From Constrained Delaunay Triangulations to Roadmap Graphs with Arbitrary Clearance

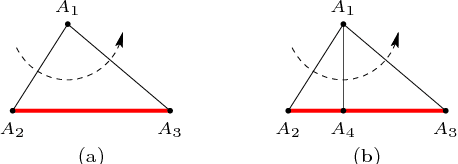
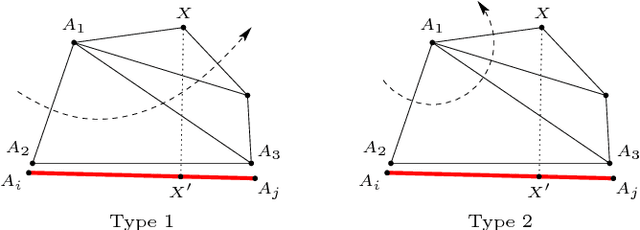
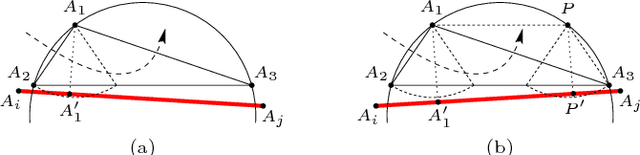
This work studies path planning in two-dimensional space, in the presence of polygonal obstacles. We specifically address the problem of building a roadmap graph, that is, an abstract representation of all the paths that can potentially be followed around a given set of obstacles. Our solution consists in an original refinement algorithm for constrained Delaunay triangulations, aimed at generating a roadmap graph suited for planning paths with arbitrary clearance. In other words, a minimum distance to the obstacles can be specified, and the graph does not have to be recomputed if this distance is modified. Compared to other solutions, our approach has the advantage of being simpler, as well as significantly more efficient.

Efficient Path Interpolation and Speed Profile Computation for Nonholonomic Mobile Robots

This paper studies path synthesis for nonholonomic mobile robots moving in two-dimensional space. We first address the problem of interpolating paths expressed as sequences of straight line segments, such as those produced by some planning algorithms, into smooth curves that can be followed without stopping. Our solution has the advantage of being simpler than other existing approaches, and has a low computational cost that allows a real-time implementation. It produces discretized paths on which curvature and variation of curvature are bounded at all points, and preserves obstacle clearance. Then, we consider the problem of computing a time-optimal speed profile for such paths. We introduce an algorithm that solves this problem in linear time, and that is able to take into account a broader class of physical constraints than other solutions. Our contributions have been implemented and evaluated in the framework of the Eurobot contest.

Min Max Generalization for Two-stage Deterministic Batch Mode Reinforcement Learning: Relaxation Schemes

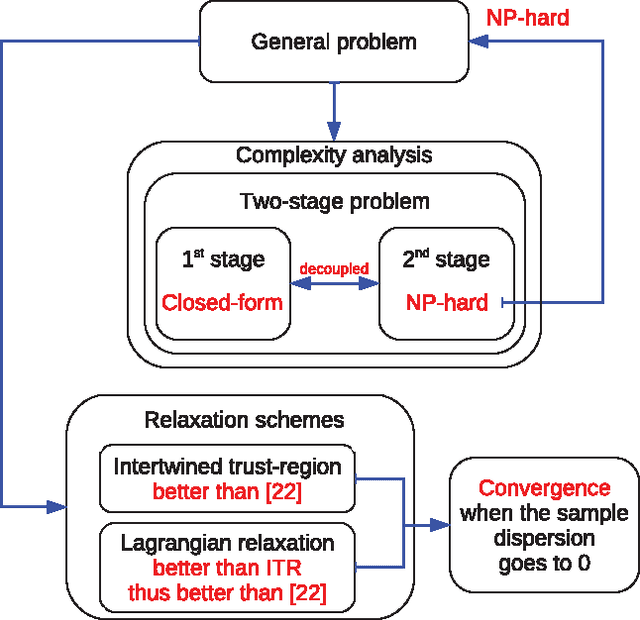
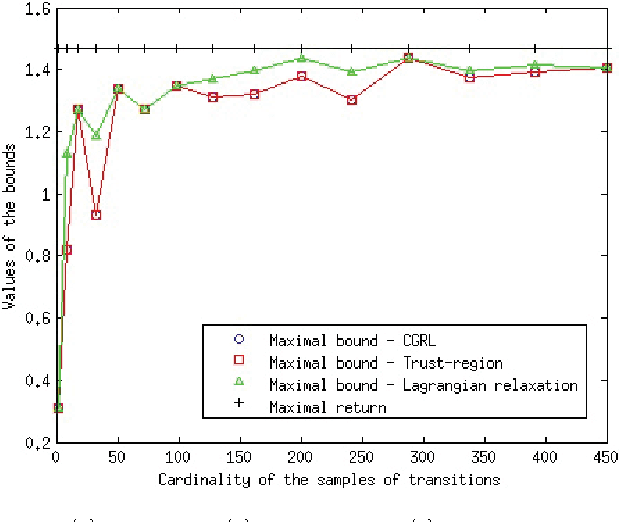
We study the minmax optimization problem introduced in [22] for computing policies for batch mode reinforcement learning in a deterministic setting. First, we show that this problem is NP-hard. In the two-stage case, we provide two relaxation schemes. The first relaxation scheme works by dropping some constraints in order to obtain a problem that is solvable in polynomial time. The second relaxation scheme, based on a Lagrangian relaxation where all constraints are dualized, leads to a conic quadratic programming problem. We also theoretically prove and empirically illustrate that both relaxation schemes provide better results than those given in [22].