From Constrained Delaunay Triangulations to Roadmap Graphs with Arbitrary Clearance
Paper and Code
Jun 07, 2016
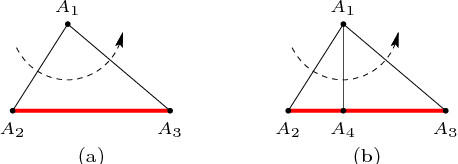
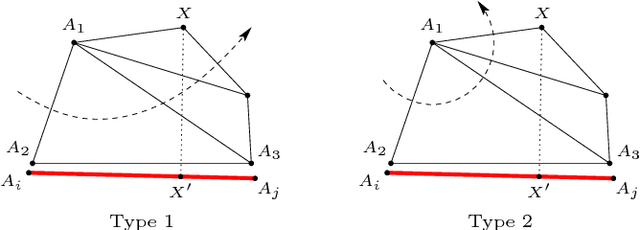
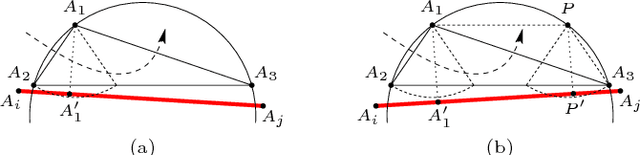
This work studies path planning in two-dimensional space, in the presence of polygonal obstacles. We specifically address the problem of building a roadmap graph, that is, an abstract representation of all the paths that can potentially be followed around a given set of obstacles. Our solution consists in an original refinement algorithm for constrained Delaunay triangulations, aimed at generating a roadmap graph suited for planning paths with arbitrary clearance. In other words, a minimum distance to the obstacles can be specified, and the graph does not have to be recomputed if this distance is modified. Compared to other solutions, our approach has the advantage of being simpler, as well as significantly more efficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge