Investigating the Monte-Carlo Tree Search Approach for the Job Shop Scheduling Problem

The Job Shop Scheduling Problem (JSSP) is a well-known optimization problem in manufacturing, where the goal is to determine the optimal sequence of jobs across different machines to minimize a given objective. In this work, we focus on minimising the weighted sum of job completion times. We explore the potential of Monte Carlo Tree Search (MCTS), a heuristic-based reinforcement learning technique, to solve large-scale JSSPs, especially those with recirculation. We propose several Markov Decision Process (MDP) formulations to model the JSSP for the MCTS algorithm. In addition, we introduce a new synthetic benchmark derived from real manufacturing data, which captures the complexity of large, non-rectangular instances often encountered in practice. Our experimental results show that MCTS effectively produces good-quality solutions for large-scale JSSP instances, outperforming our constraint programming approach.

Min Max Generalization for Two-stage Deterministic Batch Mode Reinforcement Learning: Relaxation Schemes

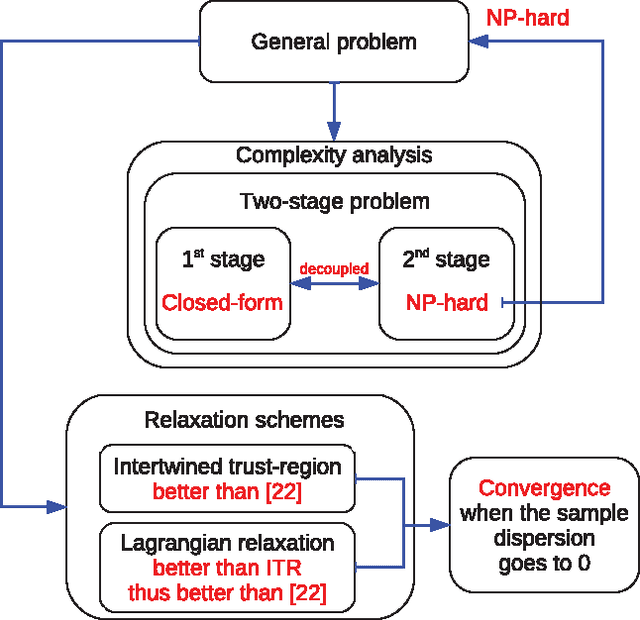
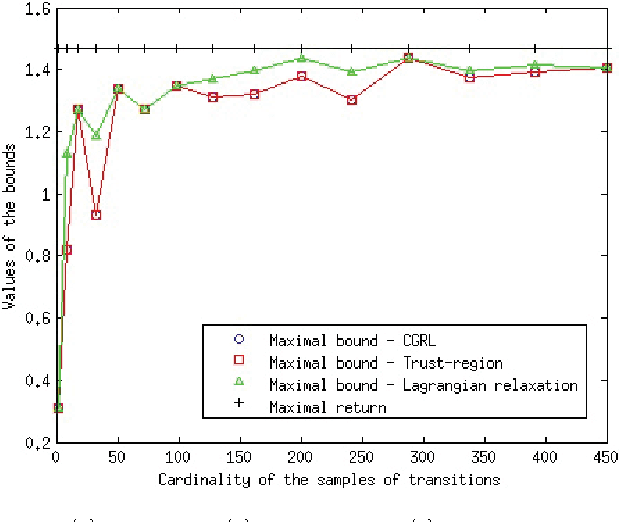
We study the minmax optimization problem introduced in [22] for computing policies for batch mode reinforcement learning in a deterministic setting. First, we show that this problem is NP-hard. In the two-stage case, we provide two relaxation schemes. The first relaxation scheme works by dropping some constraints in order to obtain a problem that is solvable in polynomial time. The second relaxation scheme, based on a Lagrangian relaxation where all constraints are dualized, leads to a conic quadratic programming problem. We also theoretically prove and empirically illustrate that both relaxation schemes provide better results than those given in [22].