On overfitting and asymptotic bias in batch reinforcement learning with partial observability
Paper and Code
Sep 22, 2017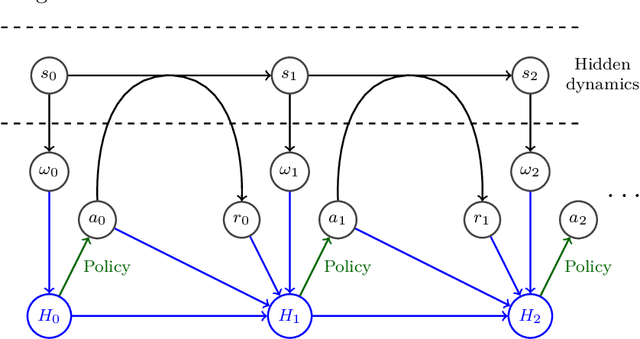

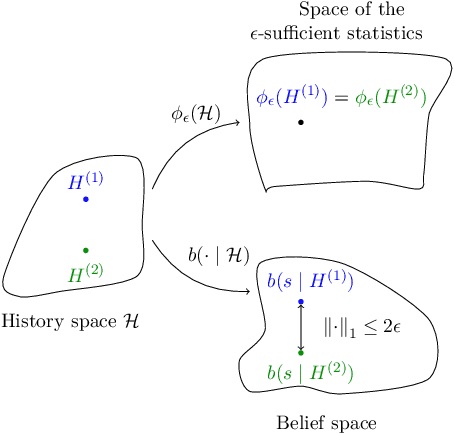
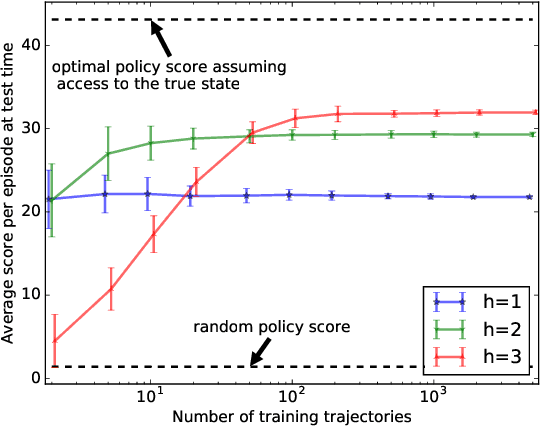
This paper stands in the context of reinforcement learning with partial observability and limited data. In this setting, we focus on the tradeoff between asymptotic bias (suboptimality with unlimited data) and overfitting (additional suboptimality due to limited data), and theoretically show that while potentially increasing the asymptotic bias, a smaller state representation decreases the risk of overfitting. Our analysis relies on expressing the quality of a state representation by bounding L1 error terms of the associated belief states. Theoretical results are empirically illustrated when the state representation is a truncated history of observations. Finally, we also discuss and empirically illustrate how using function approximators and adapting the discount factor may enhance the tradeoff between asymptotic bias and overfitting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge