How to Discount Deep Reinforcement Learning: Towards New Dynamic Strategies
Paper and Code
Jan 20, 2016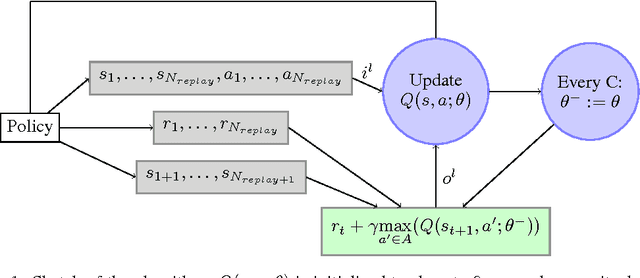
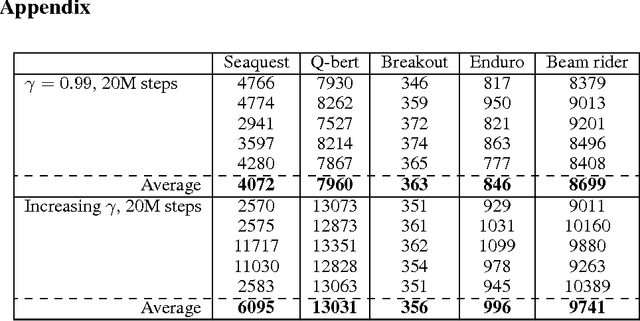
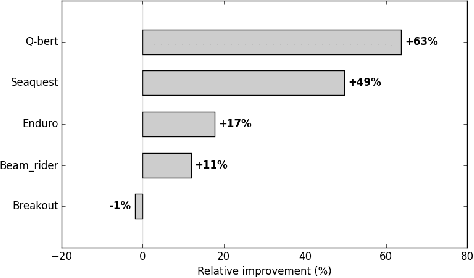

Using deep neural nets as function approximator for reinforcement learning tasks have recently been shown to be very powerful for solving problems approaching real-world complexity. Using these results as a benchmark, we discuss the role that the discount factor may play in the quality of the learning process of a deep Q-network (DQN). When the discount factor progressively increases up to its final value, we empirically show that it is possible to significantly reduce the number of learning steps. When used in conjunction with a varying learning rate, we empirically show that it outperforms original DQN on several experiments. We relate this phenomenon with the instabilities of neural networks when they are used in an approximate Dynamic Programming setting. We also describe the possibility to fall within a local optimum during the learning process, thus connecting our discussion with the exploration/exploitation dilemma.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge