Reinforcement Learning-Based Co-Design and Operation of Chiller and Thermal Energy Storage for Cost-Optimal HVAC Systems

We study the joint operation and sizing of cooling infrastructure for commercial HVAC systems using reinforcement learning, with the objective of minimizing life-cycle cost over a 30-year horizon. The cooling system consists of a fixed-capacity electric chiller and a thermal energy storage (TES) unit, jointly operated to meet stochastic hourly cooling demands under time-varying electricity prices. The life-cycle cost accounts for both capital expenditure and discounted operating cost, including electricity consumption and maintenance. A key challenge arises from the strong asymmetry in capital costs: increasing chiller capacity by one unit is far more expensive than an equivalent increase in TES capacity. As a result, identifying the right combination of chiller and TES sizes, while ensuring zero loss-of-cooling-load under optimal operation, is a non-trivial co-design problem. To address this, we formulate the chiller operation problem for a fixed infrastructure configuration as a finite-horizon Markov Decision Process (MDP), in which the control action is the chiller part-load ratio (PLR). The MDP is solved using a Deep Q Network (DQN) with a constrained action space. The learned DQN RL policy minimizes electricity cost over historical traces of cooling demand and electricity prices. For each candidate chiller-TES sizing configuration, the trained policy is evaluated. We then restrict attention to configurations that fully satisfy the cooling demand and perform a life-cycle cost minimization over this feasible set to identify the cost-optimal infrastructure design. Using this approach, we determine the optimal chiller and thermal energy storage capacities to be 700 and 1500, respectively.

Degradation-Aware Frequency Regulation of a Heterogeneous Battery Fleet via Reinforcement Learning

Battery energy storage systems are increasingly deployed as fast-responding resources for grid balancing services such as frequency regulation and for mitigating renewable generation uncertainty. However, repeated charging and discharging induces cycling degradation and reduces battery lifetime. This paper studies the real-time scheduling of a heterogeneous battery fleet that collectively tracks a stochastic balancing signal subject to per-battery ramp-rate and capacity constraints, while minimizing long-term cycling degradation. Cycling degradation is fundamentally path-dependent: it is determined by charge-discharge cycles formed by the state-of-charge (SoC) trajectory and is commonly quantified via rainflow cycle counting. This non-Markovian structure makes it difficult to express degradation as an additive per-time-step cost, complicating classical dynamic programming approaches. We address this challenge by formulating the fleet scheduling problem as a Markov decision process (MDP) with constrained action space and designing a dense proxy reward that provides informative feedback at each time step while remaining aligned with long-term cycle-depth reduction. To scale learning to large state-action spaces induced by fine-grained SoC discretization and asymmetric per-battery constraints, we develop a function-approximation reinforcement learning method using an Extreme Learning Machine (ELM) as a random nonlinear feature map combined with linear temporal-difference learning. We evaluate the proposed approach on a toy Markovian signal model and on a Markovian model trained from real-world regulation signal traces obtained from the University of Delaware, and demonstrate consistent reductions in cycle-depth occurrence and degradation metrics compared to baseline scheduling policies.

Optimal Cycling of a Heterogenous Battery Bank via Reinforcement Learning

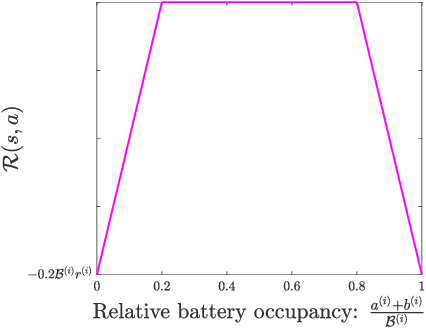
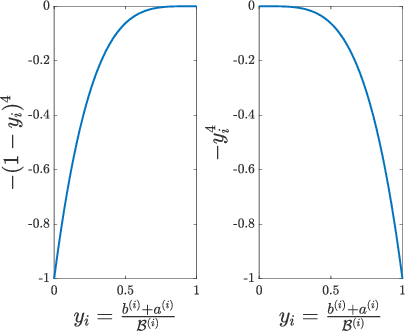
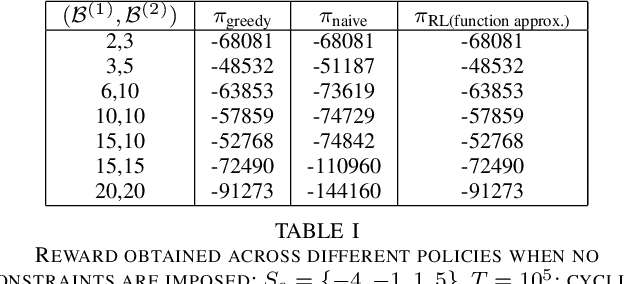
We consider the problem of optimal charging/discharging of a bank of heterogenous battery units, driven by stochastic electricity generation and demand processes. The batteries in the battery bank may differ with respect to their capacities, ramp constraints, losses, as well as cycling costs. The goal is to minimize the degradation costs associated with battery cycling in the long run; this is posed formally as a Markov decision process. We propose a linear function approximation based Q-learning algorithm for learning the optimal solution, using a specially designed class of kernel functions that approximate the structure of the value functions associated with the MDP. The proposed algorithm is validated via an extensive case study.