P. N. Karthik
Optimal Multi-Objective Best Arm Identification with Fixed Confidence
Jan 23, 2025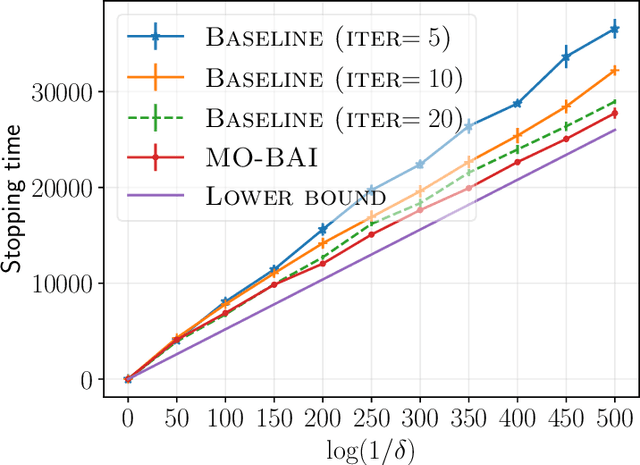

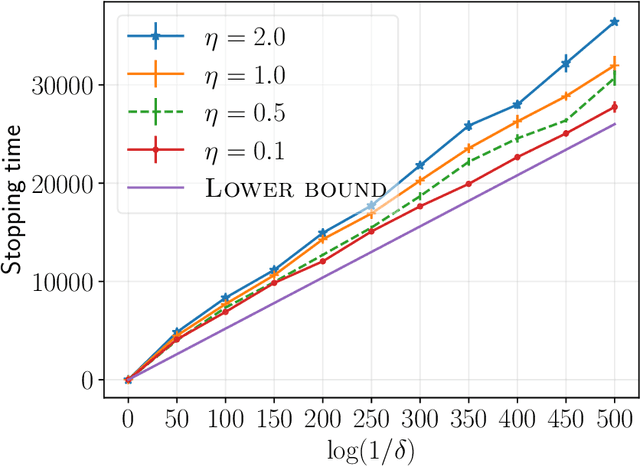

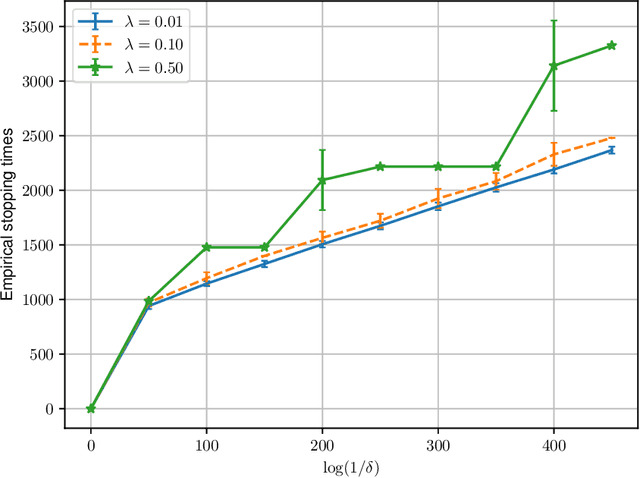
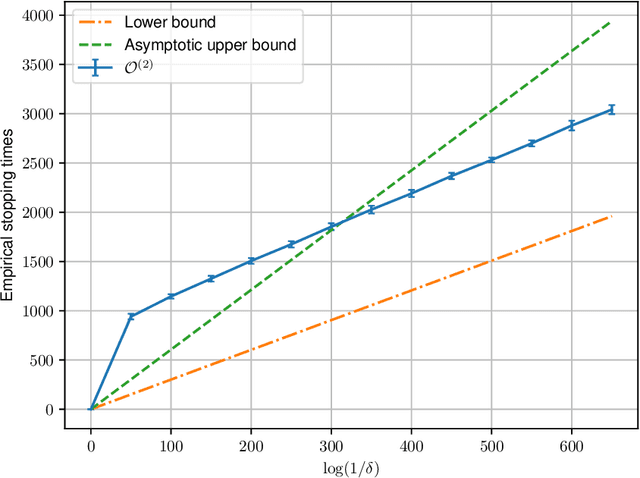
Abstract:We consider a multi-armed bandit setting with finitely many arms, in which each arm yields an $M$-dimensional vector reward upon selection. We assume that the reward of each dimension (a.k.a. {\em objective}) is generated independently of the others. The best arm of any given objective is the arm with the largest component of mean corresponding to the objective. The end goal is to identify the best arm of {\em every} objective in the shortest (expected) time subject to an upper bound on the probability of error (i.e., fixed-confidence regime). We establish a problem-dependent lower bound on the limiting growth rate of the expected stopping time, in the limit of vanishing error probabilities. This lower bound, we show, is characterised by a max-min optimisation problem that is computationally expensive to solve at each time step. We propose an algorithm that uses the novel idea of {\em surrogate proportions} to sample the arms at each time step, eliminating the need to solve the max-min optimisation problem at each step. We demonstrate theoretically that our algorithm is asymptotically optimal. In addition, we provide extensive empirical studies to substantiate the efficiency of our algorithm. While existing works on pure exploration with multi-objective multi-armed bandits predominantly focus on {\em Pareto frontier identification}, our work fills the gap in the literature by conducting a formal investigation of the multi-objective best arm identification problem.
Fixed-Budget Differentially Private Best Arm Identification
Jan 17, 2024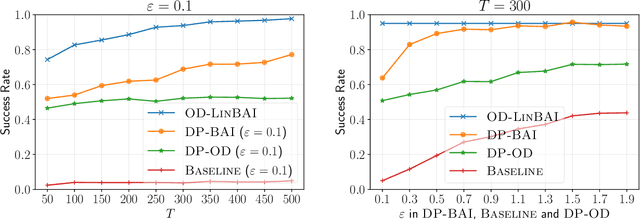

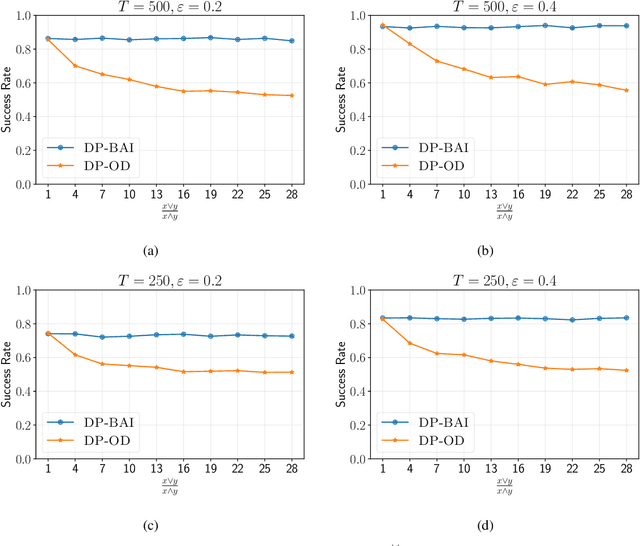
Abstract:We study best arm identification (BAI) in linear bandits in the fixed-budget regime under differential privacy constraints, when the arm rewards are supported on the unit interval. Given a finite budget $T$ and a privacy parameter $\varepsilon>0$, the goal is to minimise the error probability in finding the arm with the largest mean after $T$ sampling rounds, subject to the constraint that the policy of the decision maker satisfies a certain {\em $\varepsilon$-differential privacy} ($\varepsilon$-DP) constraint. We construct a policy satisfying the $\varepsilon$-DP constraint (called {\sc DP-BAI}) by proposing the principle of {\em maximum absolute determinants}, and derive an upper bound on its error probability. Furthermore, we derive a minimax lower bound on the error probability, and demonstrate that the lower and the upper bounds decay exponentially in $T$, with exponents in the two bounds matching order-wise in (a) the sub-optimality gaps of the arms, (b) $\varepsilon$, and (c) the problem complexity that is expressible as the sum of two terms, one characterising the complexity of standard fixed-budget BAI (without privacy constraints), and the other accounting for the $\varepsilon$-DP constraint. Additionally, we present some auxiliary results that contribute to the derivation of the lower bound on the error probability. These results, we posit, may be of independent interest and could prove instrumental in proving lower bounds on error probabilities in several other bandit problems. Whereas prior works provide results for BAI in the fixed-budget regime without privacy constraints or in the fixed-confidence regime with privacy constraints, our work fills the gap in the literature by providing the results for BAI in the fixed-budget regime under the $\varepsilon$-DP constraint.
Optimal Best Arm Identification with Fixed Confidence in Restless Bandits
Oct 20, 2023
Abstract:We study best arm identification in a restless multi-armed bandit setting with finitely many arms. The discrete-time data generated by each arm forms a homogeneous Markov chain taking values in a common, finite state space. The state transitions in each arm are captured by an ergodic transition probability matrix (TPM) that is a member of a single-parameter exponential family of TPMs. The real-valued parameters of the arm TPMs are unknown and belong to a given space. Given a function $f$ defined on the common state space of the arms, the goal is to identify the best arm -- the arm with the largest average value of $f$ evaluated under the arm's stationary distribution -- with the fewest number of samples, subject to an upper bound on the decision's error probability (i.e., the fixed-confidence regime). A lower bound on the growth rate of the expected stopping time is established in the asymptote of a vanishing error probability. Furthermore, a policy for best arm identification is proposed, and its expected stopping time is proved to have an asymptotic growth rate that matches the lower bound. It is demonstrated that tracking the long-term behavior of a certain Markov decision process and its state-action visitation proportions are the key ingredients in analyzing the converse and achievability bounds. It is shown that under every policy, the state-action visitation proportions satisfy a specific approximate flow conservation constraint and that these proportions match the optimal proportions dictated by the lower bound under any asymptotically optimal policy. The prior studies on best arm identification in restless bandits focus on independent observations from the arms, rested Markov arms, and restless Markov arms with known arm TPMs. In contrast, this work is the first to study best arm identification in restless bandits with unknown arm TPMs.
Best Arm Identification in Bandits with Limited Precision Sampling
May 10, 2023Abstract:We study best arm identification in a variant of the multi-armed bandit problem where the learner has limited precision in arm selection. The learner can only sample arms via certain exploration bundles, which we refer to as boxes. In particular, at each sampling epoch, the learner selects a box, which in turn causes an arm to get pulled as per a box-specific probability distribution. The pulled arm and its instantaneous reward are revealed to the learner, whose goal is to find the best arm by minimising the expected stopping time, subject to an upper bound on the error probability. We present an asymptotic lower bound on the expected stopping time, which holds as the error probability vanishes. We show that the optimal allocation suggested by the lower bound is, in general, non-unique and therefore challenging to track. We propose a modified tracking-based algorithm to handle non-unique optimal allocations, and demonstrate that it is asymptotically optimal. We also present non-asymptotic lower and upper bounds on the stopping time in the simpler setting when the arms accessible from one box do not overlap with those of others.
Federated Best Arm Identification with Heterogeneous Clients
Oct 17, 2022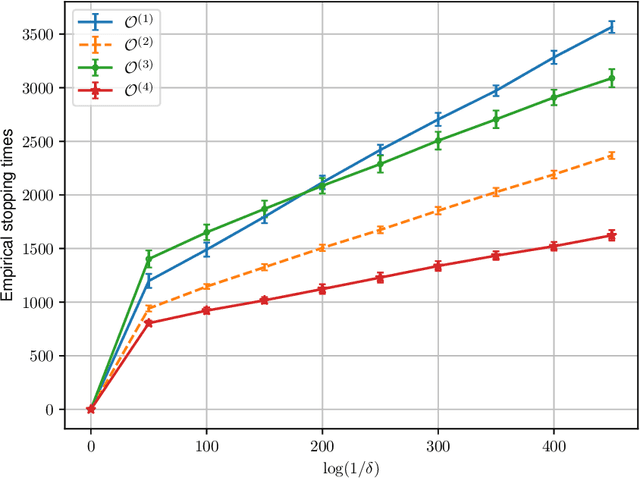
Abstract:We study best arm identification in a federated multi-armed bandit setting with a central server and multiple clients, when each client has access to a {\em subset} of arms and each arm yields independent Gaussian observations. The {\em reward} from an arm at any given time is defined as the average of the observations generated at this time across all the clients that have access to the arm. The end goal is to identify the best arm (the arm with the largest mean reward) of each client with the least expected stopping time, subject to an upper bound on the error probability (i.e., the {\em fixed-confidence regime}). We provide a lower bound on the growth rate of the expected time to find the best arm of each client. Furthermore, we show that for any algorithm whose upper bound on the expected time to find the best arms matches with the lower bound up to a multiplicative constant, the ratio of any two consecutive communication time instants must be bounded, a result that is of independent interest. We then provide the first-known lower bound on the expected number of {\em communication rounds} required to find the best arms. We propose a novel algorithm based on the well-known {\em Track-and-Stop} strategy that communicates only at exponential time instants, and derive asymptotic upper bounds on its expected time to find the best arms and the expected number of communication rounds, where the asymptotics is one of vanishing error probabilities.
Almost Cost-Free Communication in Federated Best Arm Identification
Aug 19, 2022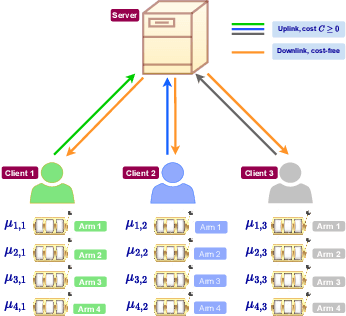

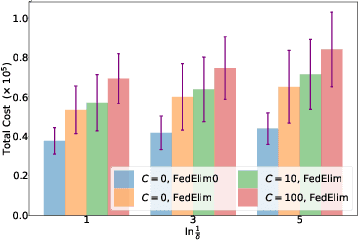
Abstract:We study the problem of best arm identification in a federated learning multi-armed bandit setup with a central server and multiple clients. Each client is associated with a multi-armed bandit in which each arm yields {\em i.i.d.}\ rewards following a Gaussian distribution with an unknown mean and known variance. The set of arms is assumed to be the same at all the clients. We define two notions of best arm -- local and global. The local best arm at a client is the arm with the largest mean among the arms local to the client, whereas the global best arm is the arm with the largest average mean across all the clients. We assume that each client can only observe the rewards from its local arms and thereby estimate its local best arm. The clients communicate with a central server on uplinks that entail a cost of $C\ge0$ units per usage per uplink. The global best arm is estimated at the server. The goal is to identify the local best arms and the global best arm with minimal total cost, defined as the sum of the total number of arm selections at all the clients and the total communication cost, subject to an upper bound on the error probability. We propose a novel algorithm {\sc FedElim} that is based on successive elimination and communicates only in exponential time steps and obtain a high probability instance-dependent upper bound on its total cost. The key takeaway from our paper is that for any $C\geq 0$ and error probabilities sufficiently small, the total number of arm selections (resp.\ the total cost) under {\sc FedElim} is at most~$2$ (resp.~$3$) times the maximum total number of arm selections under its variant that communicates in every time step. Additionally, we show that the latter is optimal in expectation up to a constant factor, thereby demonstrating that communication is almost cost-free in {\sc FedElim}. We numerically validate the efficacy of {\sc FedElim}.
Best Arm Identification in Restless Markov Multi-Armed Bandits
Mar 29, 2022Abstract:We study the problem of identifying the best arm in a multi-armed bandit environment when each arm is a time-homogeneous and ergodic discrete-time Markov process on a common, finite state space. The state evolution on each arm is governed by the arm's transition probability matrix (TPM). A decision entity that knows the set of arm TPMs but not the exact mapping of the TPMs to the arms, wishes to find the index of the best arm as quickly as possible, subject to an upper bound on the error probability. The decision entity selects one arm at a time sequentially, and all the unselected arms continue to undergo state evolution ({\em restless} arms). For this problem, we derive the first-known problem instance-dependent asymptotic lower bound on the growth rate of the expected time required to find the index of the best arm, where the asymptotics is as the error probability vanishes. Further, we propose a sequential policy that, for an input parameter $R$, forcibly selects an arm that has not been selected for $R$ consecutive time instants. We show that this policy achieves an upper bound that depends on $R$ and is monotonically non-increasing as $R\to\infty$. The question of whether, in general, the limiting value of the upper bound as $R\to\infty$ matches with the lower bound, remains open. We identify a special case in which the upper and the lower bounds match. Prior works on best arm identification have dealt with (a) independent and identically distributed observations from the arms, and (b) rested Markov arms, whereas our work deals with the more difficult setting of restless Markov arms.
Learning to Detect an Odd Restless Markov Arm with a Trembling Hand
Jun 01, 2021Abstract:This paper studies the problem of finding an anomalous arm in a multi-armed bandit when (a) each arm is a finite-state Markov process, and (b) the arms are restless. Here, anomaly means that the transition probability matrix (TPM) of one of the arms (the odd arm) is different from the common TPM of each of the non-odd arms. The TPMs are unknown to a decision entity that wishes to find the index of the odd arm as quickly as possible, subject to an upper bound on the error probability. We derive a problem instance-specific asymptotic lower bound on the expected time required to find the odd arm index, where the asymptotics is as the error probability vanishes. Further, we devise a policy based on the principle of certainty equivalence, and demonstrate that under a continuous selection assumption and a certain regularity assumption on the TPMs, the policy achieves the lower bound arbitrarily closely. Thus, while the lower bound is shown for all problem instances, the upper bound is shown only for those problem instances satisfying the continuous selection and the regularity assumptions. Our achievability analysis is based on resolving the identifiability problem in the context of a certain lifted countable-state controlled Markov process.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge