Rajesh Sundaresan
ECE
Learning to Detect an Odd Restless Markov Arm with a Trembling Hand
Jun 01, 2021Abstract:This paper studies the problem of finding an anomalous arm in a multi-armed bandit when (a) each arm is a finite-state Markov process, and (b) the arms are restless. Here, anomaly means that the transition probability matrix (TPM) of one of the arms (the odd arm) is different from the common TPM of each of the non-odd arms. The TPMs are unknown to a decision entity that wishes to find the index of the odd arm as quickly as possible, subject to an upper bound on the error probability. We derive a problem instance-specific asymptotic lower bound on the expected time required to find the odd arm index, where the asymptotics is as the error probability vanishes. Further, we devise a policy based on the principle of certainty equivalence, and demonstrate that under a continuous selection assumption and a certain regularity assumption on the TPMs, the policy achieves the lower bound arbitrarily closely. Thus, while the lower bound is shown for all problem instances, the upper bound is shown only for those problem instances satisfying the continuous selection and the regularity assumptions. Our achievability analysis is based on resolving the identifiability problem in the context of a certain lifted countable-state controlled Markov process.
Detecting an Odd Restless Markov Arm with a Trembling Hand
May 13, 2020
Abstract:In this paper, we consider a multi-armed bandit in which each arm is a Markov process evolving on a finite state space. The state space is common across the arms, and the arms are independent of each other. The transition probability matrix of one of the arms (the odd arm) is different from the common transition probability matrix of all the other arms. A decision maker, who knows these transition probability matrices, wishes to identify the odd arm as quickly as possible, while keeping the probability of decision error small. To do so, the decision maker collects observations from the arms by pulling the arms in a sequential manner, one at each discrete time instant. However, the decision maker has a trembling hand, and the arm that is actually pulled at any given time differs, with a small probability, from the one he intended to pull. The observation at any given time is the arm that is actually pulled and its current state. The Markov processes of the unobserved arms continue to evolve. This makes the arms restless. For the above setting, we derive the first known asymptotic lower bound on the expected stopping time, where the asymptotics is of vanishing error probability. The continued evolution of each arm adds a new dimension to the problem, leading to a family of Markov decision problems (MDPs) on a countable state space. We then stitch together certain parameterised solutions to these MDPs and obtain a sequence of strategies whose expected stopping times come arbitrarily close to the lower bound in the regime of vanishing error probability. Prior works dealt with independent and identically distributed (across time) arms and rested Markov arms, whereas our work deals with restless Markov arms.
The Power of Side-information in Subgraph Detection
Mar 06, 2017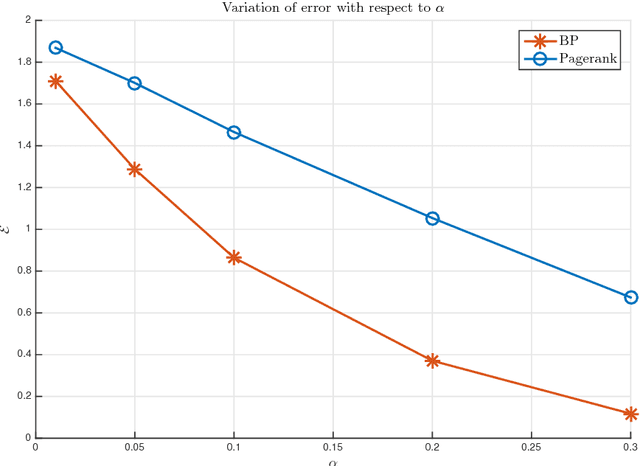
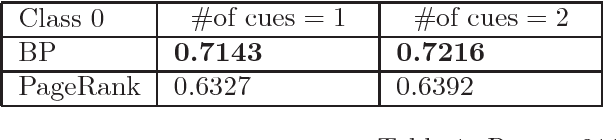
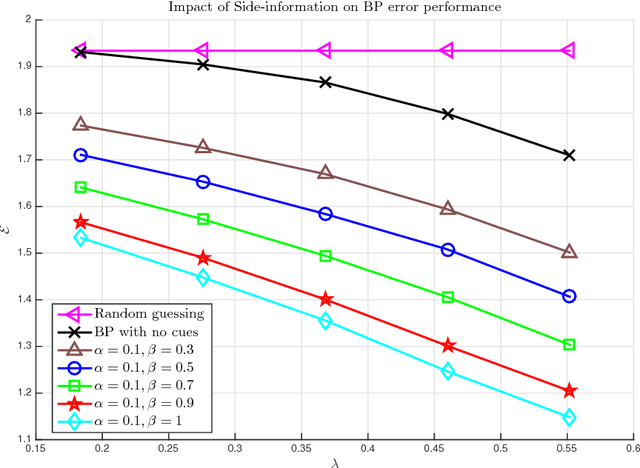
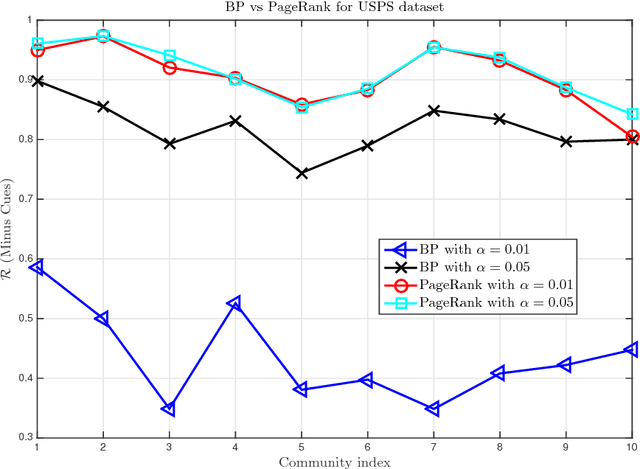
Abstract:In this work, we tackle the problem of hidden community detection. We consider Belief Propagation (BP) applied to the problem of detecting a hidden Erd\H{o}s-R\'enyi (ER) graph embedded in a larger and sparser ER graph, in the presence of side-information. We derive two related algorithms based on BP to perform subgraph detection in the presence of two kinds of side-information. The first variant of side-information consists of a set of nodes, called cues, known to be from the subgraph. The second variant of side-information consists of a set of nodes that are cues with a given probability. It was shown in past works that BP without side-information fails to detect the subgraph correctly when an effective signal-to-noise ratio (SNR) parameter falls below a threshold. In contrast, in the presence of non-trivial side-information, we show that the BP algorithm achieves asymptotically zero error for any value of the SNR parameter. We validate our results through simulations on synthetic datasets as well as on a few real world networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge