Preference-centric Bandits: Optimality of Mixtures and Regret-efficient Algorithms

The objective of canonical multi-armed bandits is to identify and repeatedly select an arm with the largest reward, often in the form of the expected value of the arm's probability distribution. Such a utilitarian perspective and focus on the probability models' first moments, however, is agnostic to the distributions' tail behavior and their implications for variability and risks in decision-making. This paper introduces a principled framework for shifting from expectation-based evaluation to an alternative reward formulation, termed a preference metric (PM). The PMs can place the desired emphasis on different reward realization and can encode a richer modeling of preferences that incorporate risk aversion, robustness, or other desired attitudes toward uncertainty. A fundamentally distinct observation in such a PM-centric perspective is that designing bandit algorithms will have a significantly different principle: as opposed to the reward-based models in which the optimal sampling policy converges to repeatedly sampling from the single best arm, in the PM-centric framework the optimal policy converges to selecting a mix of arms based on specific mixing weights. Designing such mixture policies departs from the principles for designing bandit algorithms in significant ways, primarily because of uncountable mixture possibilities. The paper formalizes the PM-centric framework and presents two algorithm classes (horizon-dependent and anytime) that learn and track mixtures in a regret-efficient fashion. These algorithms have two distinctions from their canonical counterparts: (i) they involve an estimation routine to form reliable estimates of optimal mixtures, and (ii) they are equipped with tracking mechanisms to navigate arm selection fractions to track the optimal mixtures. These algorithms' regret guarantees are investigated under various algebraic forms of the PMs.

Risk-sensitive Bandits: Arm Mixture Optimality and Regret-efficient Algorithms

This paper introduces a general framework for risk-sensitive bandits that integrates the notions of risk-sensitive objectives by adopting a rich class of distortion riskmetrics. The introduced framework subsumes the various existing risk-sensitive models. An important and hitherto unknown observation is that for a wide range of riskmetrics, the optimal bandit policy involves selecting a mixture of arms. This is in sharp contrast to the convention in the multi-arm bandit algorithms that there is generally a solitary arm that maximizes the utility, whether purely reward-centric or risk-sensitive. This creates a major departure from the principles for designing bandit algorithms since there are uncountable mixture possibilities. The contributions of the paper are as follows: (i) it formalizes a general framework for risk-sensitive bandits, (ii) identifies standard risk-sensitive bandit models for which solitary arm selections is not optimal, (iii) and designs regret-efficient algorithms whose sampling strategies can accurately track optimal arm mixtures (when mixture is optimal) or the solitary arms (when solitary is optimal). The algorithms are shown to achieve a regret that scales according to $O((\log T/T )^{\nu})$, where $T$ is the horizon, and $\nu>0$ is a riskmetric-specific constant.

Combinatorial Multi-armed Bandits: Arm Selection via Group Testing

This paper considers the problem of combinatorial multi-armed bandits with semi-bandit feedback and a cardinality constraint on the super-arm size. Existing algorithms for solving this problem typically involve two key sub-routines: (1) a parameter estimation routine that sequentially estimates a set of base-arm parameters, and (2) a super-arm selection policy for selecting a subset of base arms deemed optimal based on these parameters. State-of-the-art algorithms assume access to an exact oracle for super-arm selection with unbounded computational power. At each instance, this oracle evaluates a list of score functions, the number of which grows as low as linearly and as high as exponentially with the number of arms. This can be prohibitive in the regime of a large number of arms. This paper introduces a novel realistic alternative to the perfect oracle. This algorithm uses a combination of group-testing for selecting the super arms and quantized Thompson sampling for parameter estimation. Under a general separability assumption on the reward function, the proposed algorithm reduces the complexity of the super-arm-selection oracle to be logarithmic in the number of base arms while achieving the same regret order as the state-of-the-art algorithms that use exact oracles. This translates to at least an exponential reduction in complexity compared to the oracle-based approaches.

Improved Bound for Robust Causal Bandits with Linear Models

This paper investigates the robustness of causal bandits (CBs) in the face of temporal model fluctuations. This setting deviates from the existing literature's widely-adopted assumption of constant causal models. The focus is on causal systems with linear structural equation models (SEMs). The SEMs and the time-varying pre- and post-interventional statistical models are all unknown and subject to variations over time. The goal is to design a sequence of interventions that incur the smallest cumulative regret compared to an oracle aware of the entire causal model and its fluctuations. A robust CB algorithm is proposed, and its cumulative regret is analyzed by establishing both upper and lower bounds on the regret. It is shown that in a graph with maximum in-degree $d$, length of the largest causal path $L$, and an aggregate model deviation $C$, the regret is upper bounded by $\tilde{\mathcal{O}}(d^{L-\frac{1}{2}}(\sqrt{T} + C))$ and lower bounded by $\Omega(d^{\frac{L}{2}-2}\max\{\sqrt{T}\; ,\; d^2C\})$. The proposed algorithm achieves nearly optimal $\tilde{\mathcal{O}}(\sqrt{T})$ regret when $C$ is $o(\sqrt{T})$, maintaining sub-linear regret for a broad range of $C$.

Robust Causal Bandits for Linear Models

Sequential design of experiments for optimizing a reward function in causal systems can be effectively modeled by the sequential design of interventions in causal bandits (CBs). In the existing literature on CBs, a critical assumption is that the causal models remain constant over time. However, this assumption does not necessarily hold in complex systems, which constantly undergo temporal model fluctuations. This paper addresses the robustness of CBs to such model fluctuations. The focus is on causal systems with linear structural equation models (SEMs). The SEMs and the time-varying pre- and post-interventional statistical models are all unknown. Cumulative regret is adopted as the design criteria, based on which the objective is to design a sequence of interventions that incur the smallest cumulative regret with respect to an oracle aware of the entire causal model and its fluctuations. First, it is established that the existing approaches fail to maintain regret sub-linearity with even a few instances of model deviation. Specifically, when the number of instances with model deviation is as few as $T^\frac{1}{2L}$, where $T$ is the time horizon and $L$ is the longest causal path in the graph, the existing algorithms will have linear regret in $T$. Next, a robust CB algorithm is designed, and its regret is analyzed, where upper and information-theoretic lower bounds on the regret are established. Specifically, in a graph with $N$ nodes and maximum degree $d$, under a general measure of model deviation $C$, the cumulative regret is upper bounded by $\tilde{\mathcal{O}}(d^{L-\frac{1}{2}}(\sqrt{NT} + NC))$ and lower bounded by $\Omega(d^{\frac{L}{2}-2}\max\{\sqrt{T},d^2C\})$. Comparing these bounds establishes that the proposed algorithm achieves nearly optimal $\tilde{\mathcal{O}}(\sqrt{T})$ regret when $C$ is $o(\sqrt{T})$ and maintains sub-linear regret for a broader range of $C$.

Optimal Best Arm Identification with Fixed Confidence in Restless Bandits

We study best arm identification in a restless multi-armed bandit setting with finitely many arms. The discrete-time data generated by each arm forms a homogeneous Markov chain taking values in a common, finite state space. The state transitions in each arm are captured by an ergodic transition probability matrix (TPM) that is a member of a single-parameter exponential family of TPMs. The real-valued parameters of the arm TPMs are unknown and belong to a given space. Given a function $f$ defined on the common state space of the arms, the goal is to identify the best arm -- the arm with the largest average value of $f$ evaluated under the arm's stationary distribution -- with the fewest number of samples, subject to an upper bound on the decision's error probability (i.e., the fixed-confidence regime). A lower bound on the growth rate of the expected stopping time is established in the asymptote of a vanishing error probability. Furthermore, a policy for best arm identification is proposed, and its expected stopping time is proved to have an asymptotic growth rate that matches the lower bound. It is demonstrated that tracking the long-term behavior of a certain Markov decision process and its state-action visitation proportions are the key ingredients in analyzing the converse and achievability bounds. It is shown that under every policy, the state-action visitation proportions satisfy a specific approximate flow conservation constraint and that these proportions match the optimal proportions dictated by the lower bound under any asymptotically optimal policy. The prior studies on best arm identification in restless bandits focus on independent observations from the arms, rested Markov arms, and restless Markov arms with known arm TPMs. In contrast, this work is the first to study best arm identification in restless bandits with unknown arm TPMs.

Best Arm Identification in Stochastic Bandits: Beyond $β-$optimality

This paper focuses on best arm identification (BAI) in stochastic multi-armed bandits (MABs) in the fixed-confidence, parametric setting. In such pure exploration problems, the accuracy of the sampling strategy critically hinges on the sequential allocation of the sampling resources among the arms. The existing approaches to BAI address the following question: what is an optimal sampling strategy when we spend a $\beta$ fraction of the samples on the best arm? These approaches treat $\beta$ as a tunable parameter and offer efficient algorithms that ensure optimality up to selecting $\beta$, hence $\beta-$optimality. However, the BAI decisions and performance can be highly sensitive to the choice of $\beta$. This paper provides a BAI algorithm that is agnostic to $\beta$, dispensing with the need for tuning $\beta$, and specifies an optimal allocation strategy, including the optimal value of $\beta$. Furthermore, the existing relevant literature focuses on the family of exponential distributions. This paper considers a more general setting of any arbitrary family of distributions parameterized by their mean values (under mild regularity conditions).

Active Sampling of Multiple Sources for Sequential Estimation

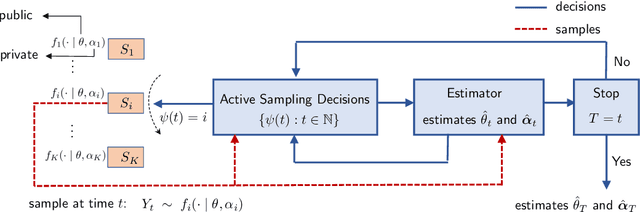
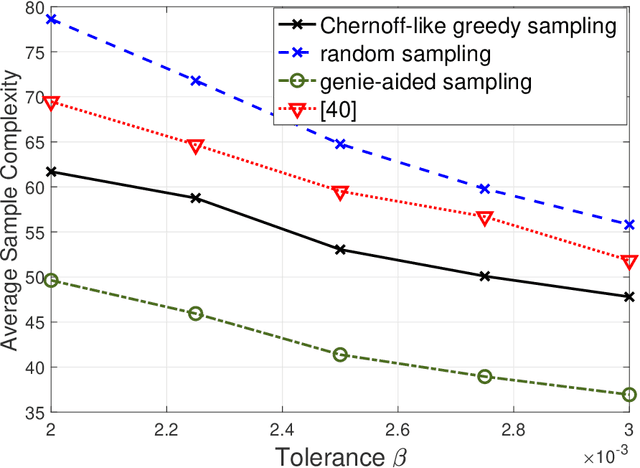
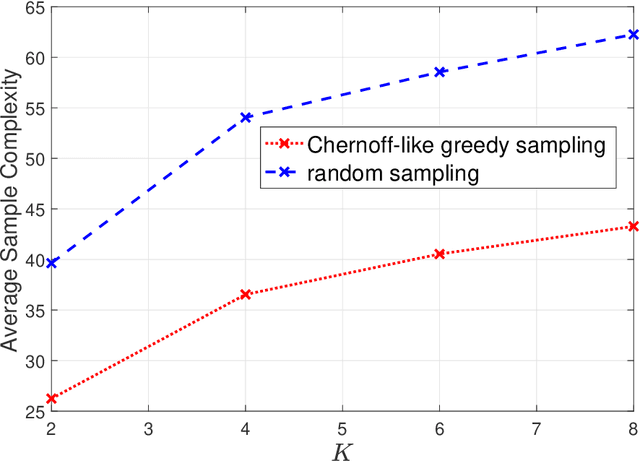
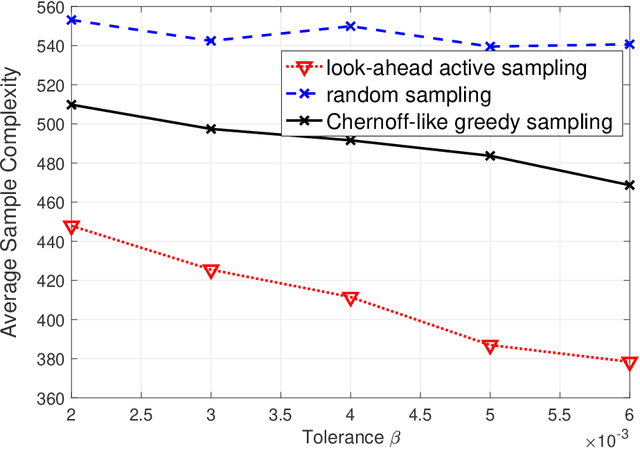
Consider $K$ processes, each generating a sequence of identical and independent random variables. The probability measures of these processes have random parameters that must be estimated. Specifically, they share a parameter $\theta$ common to all probability measures. Additionally, each process $i\in\{1, \dots, K\}$ has a private parameter $\alpha_i$. The objective is to design an active sampling algorithm for sequentially estimating these parameters in order to form reliable estimates for all shared and private parameters with the fewest number of samples. This sampling algorithm has three key components: (i)~data-driven sampling decisions, which dynamically over time specifies which of the $K$ processes should be selected for sampling; (ii)~stopping time for the process, which specifies when the accumulated data is sufficient to form reliable estimates and terminate the sampling process; and (iii)~estimators for all shared and private parameters. Owing to the sequential estimation being known to be analytically intractable, this paper adopts \emph {conditional} estimation cost functions, leading to a sequential estimation approach that was recently shown to render tractable analysis. Asymptotically optimal decision rules (sampling, stopping, and estimation) are delineated, and numerical experiments are provided to compare the efficacy and quality of the proposed procedure with those of the relevant approaches.

SPRT-based Efficient Best Arm Identification in Stochastic Bandits

This paper investigates the best arm identification (BAI) problem in stochastic multi-armed bandits in the fixed confidence setting. The general class of the exponential family of bandits is considered. The state-of-the-art algorithms for the exponential family of bandits face computational challenges. To mitigate these challenges, a novel framework is proposed, which views the BAI problem as sequential hypothesis testing, and is amenable to tractable analysis for the exponential family of bandits. Based on this framework, a BAI algorithm is designed that leverages the canonical sequential probability ratio tests. This algorithm has three features for both settings: (1) its sample complexity is asymptotically optimal, (2) it is guaranteed to be $\delta-$PAC, and (3) it addresses the computational challenge of the state-of-the-art approaches. Specifically, these approaches, which are focused only on the Gaussian setting, require Thompson sampling from the arm that is deemed the best and a challenger arm. This paper analytically shows that identifying the challenger is computationally expensive and that the proposed algorithm circumvents it. Finally, numerical experiments are provided to support the analysis.

Mean-based Best Arm Identification in Stochastic Bandits under Reward Contamination

This paper investigates the problem of best arm identification in $\textit{contaminated}$ stochastic multi-arm bandits. In this setting, the rewards obtained from any arm are replaced by samples from an adversarial model with probability $\varepsilon$. A fixed confidence (infinite-horizon) setting is considered, where the goal of the learner is to identify the arm with the largest mean. Owing to the adversarial contamination of the rewards, each arm's mean is only partially identifiable. This paper proposes two algorithms, a gap-based algorithm and one based on the successive elimination, for best arm identification in sub-Gaussian bandits. These algorithms involve mean estimates that achieve the optimal error guarantee on the deviation of the true mean from the estimate asymptotically. Furthermore, these algorithms asymptotically achieve the optimal sample complexity. Specifically, for the gap-based algorithm, the sample complexity is asymptotically optimal up to constant factors, while for the successive elimination-based algorithm, it is optimal up to logarithmic factors. Finally, numerical experiments are provided to illustrate the gains of the algorithms compared to the existing baselines.