Interventional Causal Discovery in a Mixture of DAGs

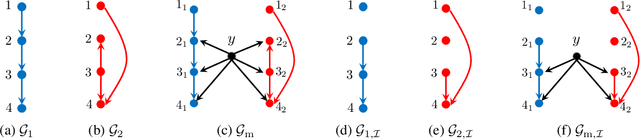
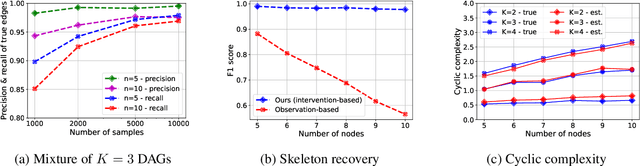
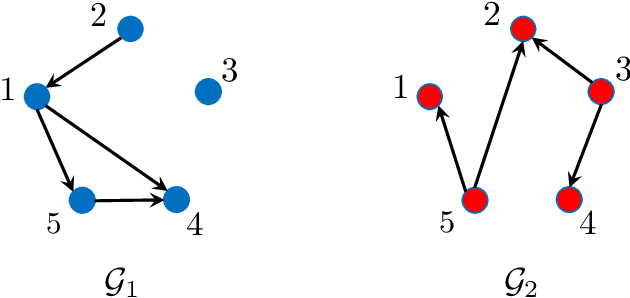
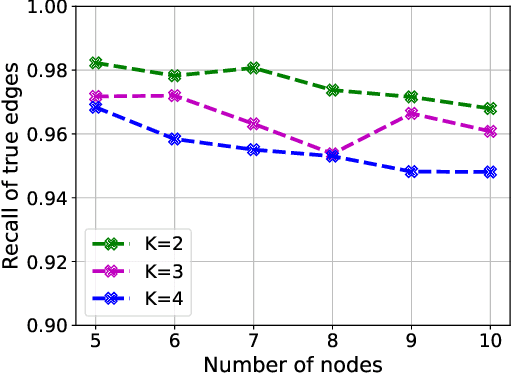
Causal interactions among a group of variables are often modeled by a single causal graph. In some domains, however, these interactions are best described by multiple co-existing causal graphs, e.g., in dynamical systems or genomics. This paper addresses the hitherto unknown role of interventions in learning causal interactions among variables governed by a mixture of causal systems, each modeled by one directed acyclic graph (DAG). Causal discovery from mixtures is fundamentally more challenging than single-DAG causal discovery. Two major difficulties stem from (i) inherent uncertainty about the skeletons of the component DAGs that constitute the mixture and (ii) possibly cyclic relationships across these component DAGs. This paper addresses these challenges and aims to identify edges that exist in at least one component DAG of the mixture, referred to as true edges. First, it establishes matching necessary and sufficient conditions on the size of interventions required to identify the true edges. Next, guided by the necessity results, an adaptive algorithm is designed that learns all true edges using ${\cal O}(n^2)$ interventions, where $n$ is the number of nodes. Remarkably, the size of the interventions is optimal if the underlying mixture model does not contain cycles across its components. More generally, the gap between the intervention size used by the algorithm and the optimal size is quantified. It is shown to be bounded by the cyclic complexity number of the mixture model, defined as the size of the minimal intervention that can break the cycles in the mixture, which is upper bounded by the number of cycles among the ancestors of a node.

Linear Causal Representation Learning from Unknown Multi-node Interventions

Despite the multifaceted recent advances in interventional causal representation learning (CRL), they primarily focus on the stylized assumption of single-node interventions. This assumption is not valid in a wide range of applications, and generally, the subset of nodes intervened in an interventional environment is fully unknown. This paper focuses on interventional CRL under unknown multi-node (UMN) interventional environments and establishes the first identifiability results for general latent causal models (parametric or nonparametric) under stochastic interventions (soft or hard) and linear transformation from the latent to observed space. Specifically, it is established that given sufficiently diverse interventional environments, (i) identifiability up to ancestors is possible using only soft interventions, and (ii) perfect identifiability is possible using hard interventions. Remarkably, these guarantees match the best-known results for more restrictive single-node interventions. Furthermore, CRL algorithms are also provided that achieve the identifiability guarantees. A central step in designing these algorithms is establishing the relationships between UMN interventional CRL and score functions associated with the statistical models of different interventional environments. Establishing these relationships also serves as constructive proof of the identifiability guarantees.

Improved Bound for Robust Causal Bandits with Linear Models

This paper investigates the robustness of causal bandits (CBs) in the face of temporal model fluctuations. This setting deviates from the existing literature's widely-adopted assumption of constant causal models. The focus is on causal systems with linear structural equation models (SEMs). The SEMs and the time-varying pre- and post-interventional statistical models are all unknown and subject to variations over time. The goal is to design a sequence of interventions that incur the smallest cumulative regret compared to an oracle aware of the entire causal model and its fluctuations. A robust CB algorithm is proposed, and its cumulative regret is analyzed by establishing both upper and lower bounds on the regret. It is shown that in a graph with maximum in-degree $d$, length of the largest causal path $L$, and an aggregate model deviation $C$, the regret is upper bounded by $\tilde{\mathcal{O}}(d^{L-\frac{1}{2}}(\sqrt{T} + C))$ and lower bounded by $\Omega(d^{\frac{L}{2}-2}\max\{\sqrt{T}\; ,\; d^2C\})$. The proposed algorithm achieves nearly optimal $\tilde{\mathcal{O}}(\sqrt{T})$ regret when $C$ is $o(\sqrt{T})$, maintaining sub-linear regret for a broad range of $C$.

Score-based Causal Representation Learning: Linear and General Transformations

This paper addresses intervention-based causal representation learning (CRL) under a general nonparametric latent causal model and an unknown transformation that maps the latent variables to the observed variables. Linear and general transformations are investigated. The paper addresses both the \emph{identifiability} and \emph{achievability} aspects. Identifiability refers to determining algorithm-agnostic conditions that ensure recovering the true latent causal variables and the latent causal graph underlying them. Achievability refers to the algorithmic aspects and addresses designing algorithms that achieve identifiability guarantees. By drawing novel connections between \emph{score functions} (i.e., the gradients of the logarithm of density functions) and CRL, this paper designs a \emph{score-based class of algorithms} that ensures both identifiability and achievability. First, the paper focuses on \emph{linear} transformations and shows that one stochastic hard intervention per node suffices to guarantee identifiability. It also provides partial identifiability guarantees for soft interventions, including identifiability up to ancestors for general causal models and perfect latent graph recovery for sufficiently non-linear causal models. Secondly, it focuses on \emph{general} transformations and shows that two stochastic hard interventions per node suffice for identifiability. Notably, one does \emph{not} need to know which pair of interventional environments have the same node intervened.

Robust Causal Bandits for Linear Models

Sequential design of experiments for optimizing a reward function in causal systems can be effectively modeled by the sequential design of interventions in causal bandits (CBs). In the existing literature on CBs, a critical assumption is that the causal models remain constant over time. However, this assumption does not necessarily hold in complex systems, which constantly undergo temporal model fluctuations. This paper addresses the robustness of CBs to such model fluctuations. The focus is on causal systems with linear structural equation models (SEMs). The SEMs and the time-varying pre- and post-interventional statistical models are all unknown. Cumulative regret is adopted as the design criteria, based on which the objective is to design a sequence of interventions that incur the smallest cumulative regret with respect to an oracle aware of the entire causal model and its fluctuations. First, it is established that the existing approaches fail to maintain regret sub-linearity with even a few instances of model deviation. Specifically, when the number of instances with model deviation is as few as $T^\frac{1}{2L}$, where $T$ is the time horizon and $L$ is the longest causal path in the graph, the existing algorithms will have linear regret in $T$. Next, a robust CB algorithm is designed, and its regret is analyzed, where upper and information-theoretic lower bounds on the regret are established. Specifically, in a graph with $N$ nodes and maximum degree $d$, under a general measure of model deviation $C$, the cumulative regret is upper bounded by $\tilde{\mathcal{O}}(d^{L-\frac{1}{2}}(\sqrt{NT} + NC))$ and lower bounded by $\Omega(d^{\frac{L}{2}-2}\max\{\sqrt{T},d^2C\})$. Comparing these bounds establishes that the proposed algorithm achieves nearly optimal $\tilde{\mathcal{O}}(\sqrt{T})$ regret when $C$ is $o(\sqrt{T})$ and maintains sub-linear regret for a broader range of $C$.

General Identifiability and Achievability for Causal Representation Learning

This paper focuses on causal representation learning (CRL) under a general nonparametric causal latent model and a general transformation model that maps the latent data to the observational data. It establishes \textbf{identifiability} and \textbf{achievability} results using two hard \textbf{uncoupled} interventions per node in the latent causal graph. Notably, one does not know which pair of intervention environments have the same node intervened (hence, uncoupled environments). For identifiability, the paper establishes that perfect recovery of the latent causal model and variables is guaranteed under uncoupled interventions. For achievability, an algorithm is designed that uses observational and interventional data and recovers the latent causal model and variables with provable guarantees for the algorithm. This algorithm leverages score variations across different environments to estimate the inverse of the transformer and, subsequently, the latent variables. The analysis, additionally, recovers the existing identifiability result for two hard \textbf{coupled} interventions, that is when metadata about the pair of environments that have the same node intervened is known. It is noteworthy that the existing results on non-parametric identifiability require assumptions on interventions and additional faithfulness assumptions. This paper shows that when observational data is available, additional faithfulness assumptions are unnecessary.