Interventional Causal Discovery in a Mixture of DAGs
Paper and Code
Jun 12, 2024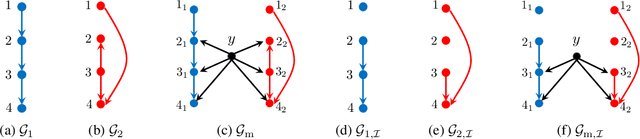
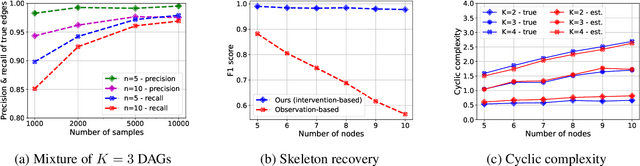
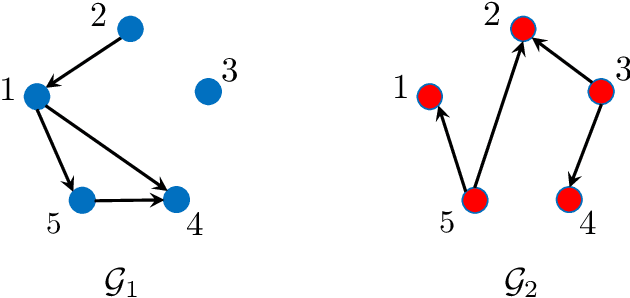
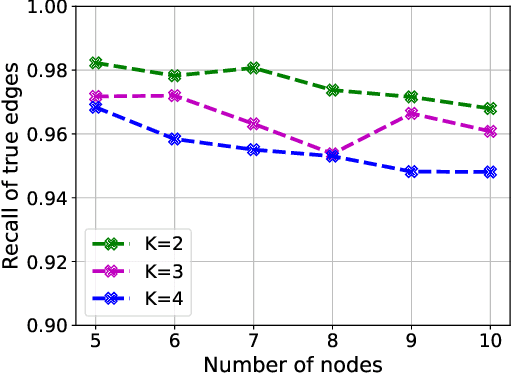
Causal interactions among a group of variables are often modeled by a single causal graph. In some domains, however, these interactions are best described by multiple co-existing causal graphs, e.g., in dynamical systems or genomics. This paper addresses the hitherto unknown role of interventions in learning causal interactions among variables governed by a mixture of causal systems, each modeled by one directed acyclic graph (DAG). Causal discovery from mixtures is fundamentally more challenging than single-DAG causal discovery. Two major difficulties stem from (i) inherent uncertainty about the skeletons of the component DAGs that constitute the mixture and (ii) possibly cyclic relationships across these component DAGs. This paper addresses these challenges and aims to identify edges that exist in at least one component DAG of the mixture, referred to as true edges. First, it establishes matching necessary and sufficient conditions on the size of interventions required to identify the true edges. Next, guided by the necessity results, an adaptive algorithm is designed that learns all true edges using ${\cal O}(n^2)$ interventions, where $n$ is the number of nodes. Remarkably, the size of the interventions is optimal if the underlying mixture model does not contain cycles across its components. More generally, the gap between the intervention size used by the algorithm and the optimal size is quantified. It is shown to be bounded by the cyclic complexity number of the mixture model, defined as the size of the minimal intervention that can break the cycles in the mixture, which is upper bounded by the number of cycles among the ancestors of a node.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge