Active Sampling of Multiple Sources for Sequential Estimation
Paper and Code
Aug 10, 2022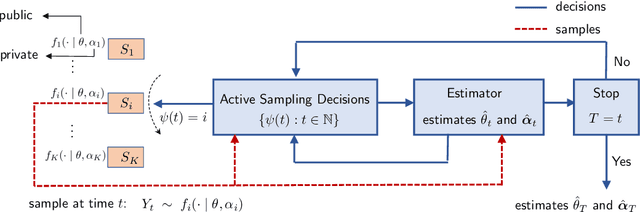
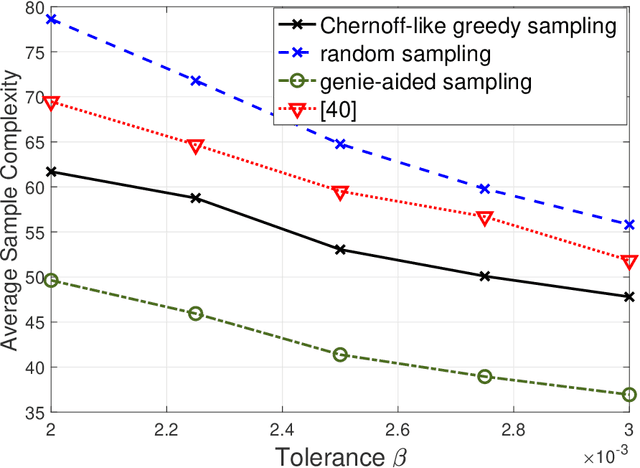
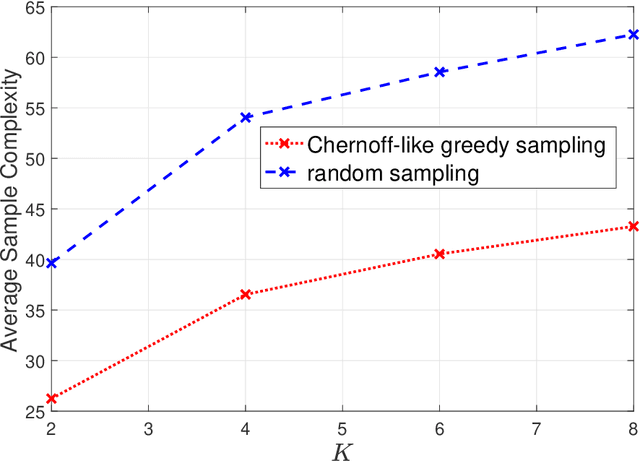
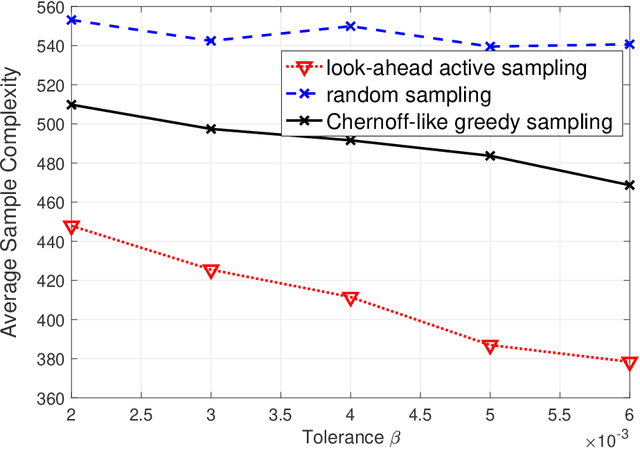
Consider $K$ processes, each generating a sequence of identical and independent random variables. The probability measures of these processes have random parameters that must be estimated. Specifically, they share a parameter $\theta$ common to all probability measures. Additionally, each process $i\in\{1, \dots, K\}$ has a private parameter $\alpha_i$. The objective is to design an active sampling algorithm for sequentially estimating these parameters in order to form reliable estimates for all shared and private parameters with the fewest number of samples. This sampling algorithm has three key components: (i)~data-driven sampling decisions, which dynamically over time specifies which of the $K$ processes should be selected for sampling; (ii)~stopping time for the process, which specifies when the accumulated data is sufficient to form reliable estimates and terminate the sampling process; and (iii)~estimators for all shared and private parameters. Owing to the sequential estimation being known to be analytically intractable, this paper adopts \emph {conditional} estimation cost functions, leading to a sequential estimation approach that was recently shown to render tractable analysis. Asymptotically optimal decision rules (sampling, stopping, and estimation) are delineated, and numerical experiments are provided to compare the efficacy and quality of the proposed procedure with those of the relevant approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge