A Parameterized Perspective on Protecting Elections

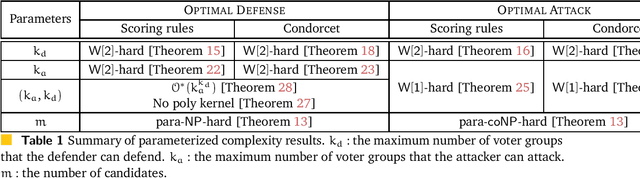
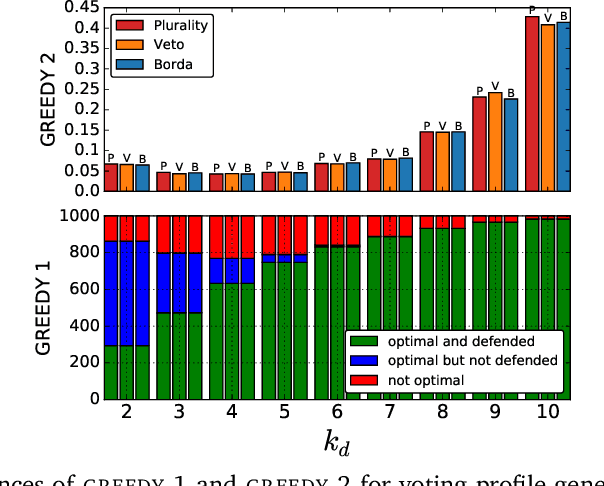
We study the parameterized complexity of the optimal defense and optimal attack problems in voting. In both the problems, the input is a set of voter groups (every voter group is a set of votes) and two integers $k_a$ and $k_d$ corresponding to respectively the number of voter groups the attacker can attack and the number of voter groups the defender can defend. A voter group gets removed from the election if it is attacked but not defended. In the optimal defense problem, we want to know if it is possible for the defender to commit to a strategy of defending at most $k_d$ voter groups such that, no matter which $k_a$ voter groups the attacker attacks, the outcome of the election does not change. In the optimal attack problem, we want to know if it is possible for the attacker to commit to a strategy of attacking $k_a$ voter groups such that, no matter which $k_d$ voter groups the defender defends, the outcome of the election is always different from the original (without any attack) one.

Testing Preferential Domains Using Sampling

A preferential domain is a collection of sets of preferences which are linear orders over a set of alternatives. These domains have been studied extensively in social choice theory due to both its practical importance and theoretical elegance. Examples of some extensively studied preferential domains include single peaked, single crossing, Euclidean, etc. In this paper, we study the sample complexity of testing whether a given preference profile is close to some specific domain. We consider two notions of closeness: (a) closeness via preferences, and (b) closeness via alternatives. We further explore the effect of assuming that the {\em outlier} preferences/alternatives to be random (instead of arbitrary) on the sample complexity of the testing problem. In most cases, we show that the above testing problem can be solved with high probability for all commonly used domains by observing only a small number of samples (independent of the number of preferences, $n$, and often the number of alternatives, $m$). In the remaining few cases, we prove either impossibility results or $\Omega(n)$ lower bound on the sample complexity. We complement our theoretical findings with extensive simulations to figure out the actual constant factors of our asymptotic sample complexity bounds.