Complexity of Manipulation with Partial Information in Voting
Paper and Code
Jul 13, 2017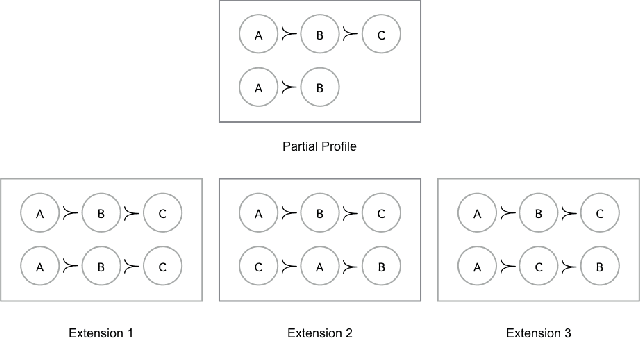
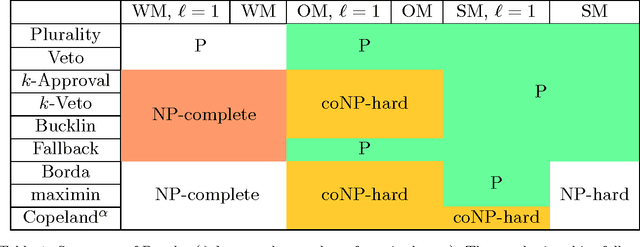

The Coalitional Manipulation problem has been studied extensively in the literature for many voting rules. However, most studies have focused on the complete information setting, wherein the manipulators know the votes of the non-manipulators. While this assumption is reasonable for purposes of showing intractability, it is unrealistic for algorithmic considerations. In most real-world scenarios, it is impractical for the manipulators to have accurate knowledge of all the other votes. In this paper, we investigate manipulation with incomplete information. In our framework, the manipulators know a partial order for each voter that is consistent with the true preference of that voter. In this setting, we formulate three natural computational notions of manipulation, namely weak, opportunistic, and strong manipulation. We say that an extension of a partial order is if there exists a manipulative vote for that extension. 1. Weak Manipulation (WM): the manipulators seek to vote in a way that makes their preferred candidate win in at least one extension of the partial votes of the non-manipulators. 2. Opportunistic Manipulation (OM): the manipulators seek to vote in a way that makes their preferred candidate win in every viable extension of the partial votes of the non-manipulators. 3. Strong Manipulation (SM): the manipulators seek to vote in a way that makes their preferred candidate win in every extension of the partial votes of the non-manipulators. We consider several scenarios for which the traditional manipulation problems are easy (for instance, Borda with a single manipulator). For many of them, the corresponding manipulative questions that we propose turn out to be computationally intractable. Our hardness results often hold even when very little information is missing, or in other words, even when the instances are quite close to the complete information setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge