A Surrogate Model for the Forward Design of Multi-layered Metasurface-based Radar Absorbing Structures

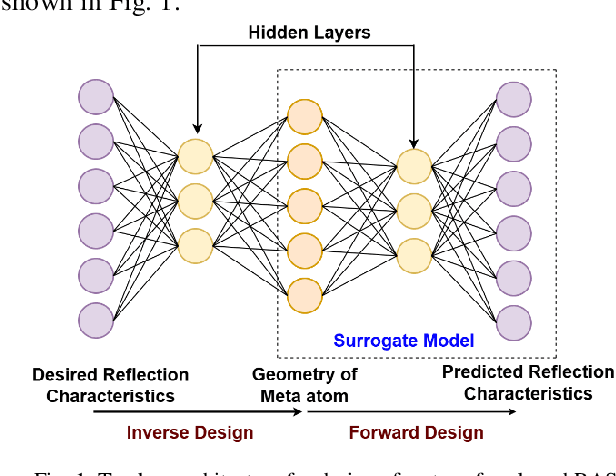
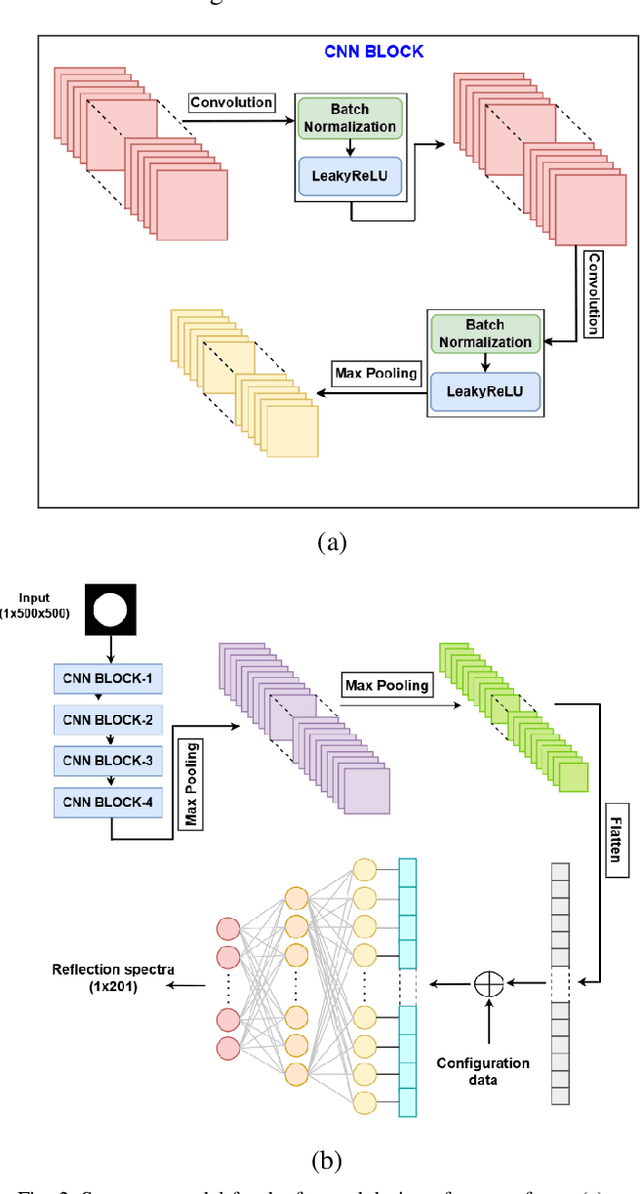
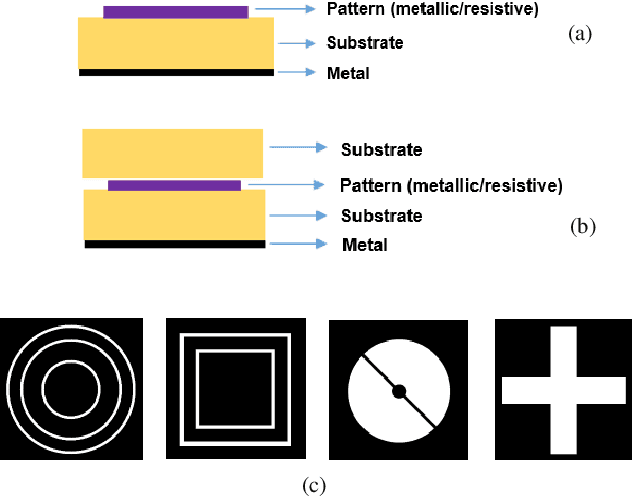
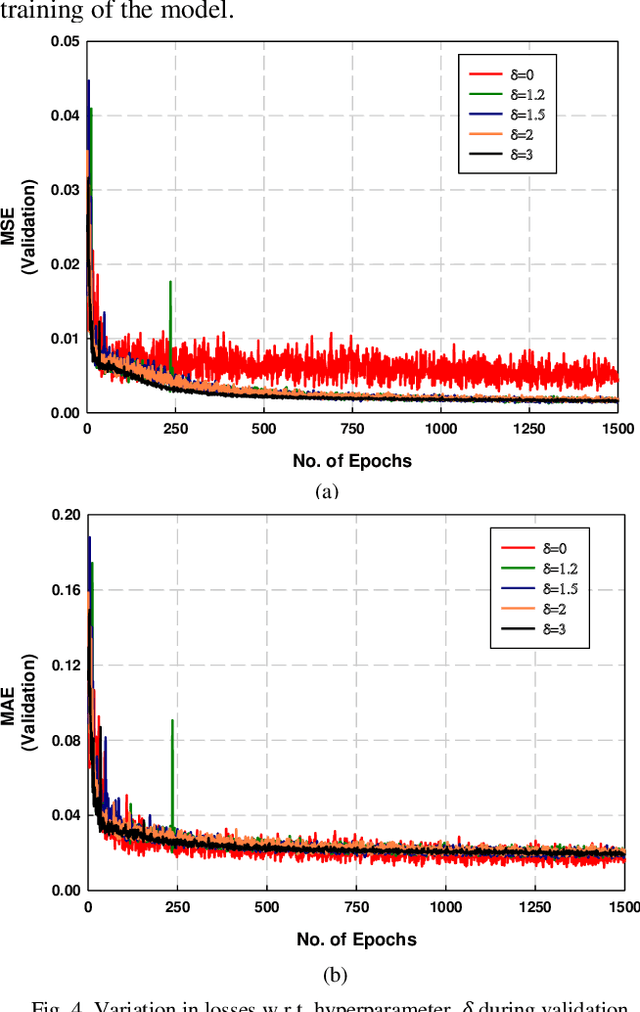
Metasurface-based radar absorbing structures (RAS) are highly preferred for applications like stealth technology, electromagnetic (EM) shielding, etc. due to their capability to achieve frequency selective absorption characteristics with minimal thickness and reduced weight penalty. However, the conventional approach for the EM design and optimization of these structures relies on forward simulations, using full wave simulation tools, to predict the electromagnetic (EM) response of candidate meta atoms. This process is computationally intensive, extremely time consuming and requires exploration of large design spaces. To overcome this challenge, we propose a surrogate model that significantly accelerates the prediction of EM responses of multi-layered metasurface-based RAS. A convolutional neural network (CNN) based architecture with Huber loss function has been employed to estimate the reflection characteristics of the RAS model. The proposed model achieved a cosine similarity of 99.9% and a mean square error of 0.001 within 1000 epochs of training. The efficiency of the model has been established via full wave simulations as well as experiment where it demonstrated significant reduction in computational time while maintaining high predictive accuracy.

Split: Inferring Unobserved Event Probabilities for Disentangling Brand-Customer Interactions

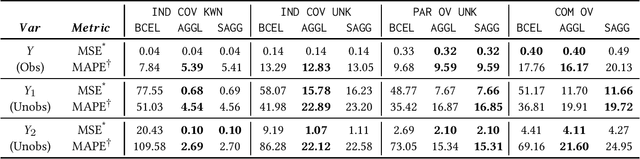
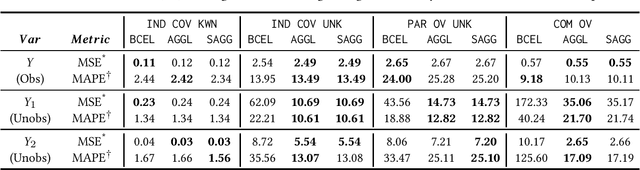
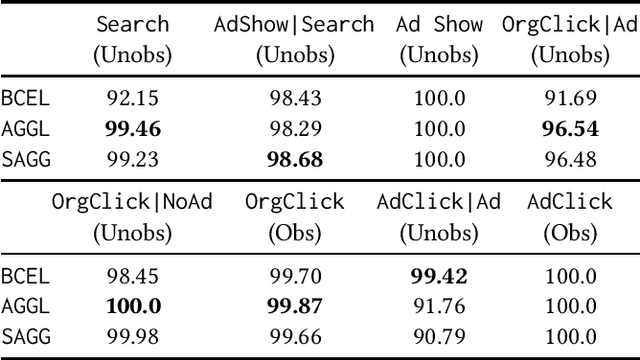
Often, data contains only composite events composed of multiple events, some observed and some unobserved. For example, search ad click is observed by a brand, whereas which customers were shown a search ad - an actionable variable - is often not observed. In such cases, inference is not possible on unobserved event. This occurs when a marketing action is taken over earned and paid digital channels. Similar setting arises in numerous datasets where multiple actors interact. One approach is to use the composite event as a proxy for the unobserved event of interest. However, this leads to invalid inference. This paper takes a direct approach whereby an event of interest is identified based on information on the composite event and aggregate data on composite events (e.g. total number of search ads shown). This work contributes to the literature by proving identification of the unobserved events' probabilities up to a scalar factor under mild condition. We propose an approach to identify the scalar factor by using aggregate data that is usually available from earned and paid channels. The factor is identified by adding a loss term to the usual cross-entropy loss. We validate the approach on three synthetic datasets. In addition, the approach is validated on a real marketing problem where some observed events are hidden from the algorithm for validation. The proposed modification to the cross-entropy loss function improves the average performance by 46%.

Stable Manipulation in Voting

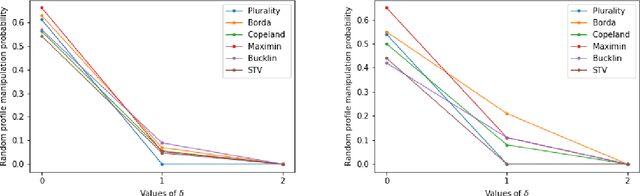
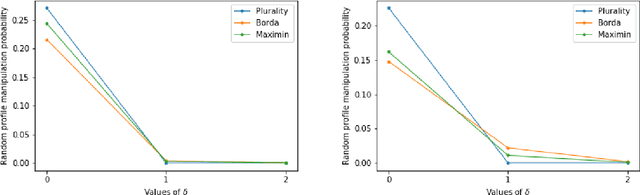
We introduce the problem of {\em stable manipulation} where the manipulators need to compute if there exist votes for the manipulators which make their preferred alternative win the election even if the manipulators' knowledge about others' votes are little inaccurate, that is, manipulation remains successful even under small perturbation of the non-manipulators' votes. We show that every scoring rule, maximin, Bucklin, and simplified Bucklin voting rules are stably manipulable in polynomial time for single manipulator. In contrast, stable manipulation becomes intractable for the Copeland$^\alpha$ voting rule for every $\alpha\in[0,1]$ even for single manipulator. However for a constant number of alternatives, we show that the stable manipulation problem is polynomial time solvable for every anonymous and efficient voting rules. Finally we empirically show that the probability that a uniformly random profile is stably manipulable decreases drastically even if manipulator possess little uncertainty about others' votes.