Sampling-Based Winner Prediction in District-Based Elections

In a district-based election, we apply a voting rule $r$ to decide the winners in each district, and a candidate who wins in a maximum number of districts is the winner of the election. We present efficient sampling-based algorithms to predict the winner of such district-based election systems in this paper. When $r$ is plurality and the margin of victory is known to be at least $\varepsilon$ fraction of the total population, we present an algorithm to predict the winner. The sample complexity of our algorithm is $\mathcal{O}\left(\frac{1}{\varepsilon^4}\log \frac{1}{\varepsilon}\log\frac{1}{\delta}\right)$. We complement this result by proving that any algorithm, from a natural class of algorithms, for predicting the winner in a district-based election when $r$ is plurality, must sample at least $\Omega\left(\frac{1}{\varepsilon^4}\log\frac{1}{\delta}\right)$ votes. We then extend this result to any voting rule $r$. Loosely speaking, we show that we can predict the winner of a district-based election with an extra overhead of $\mathcal{O}\left(\frac{1}{\varepsilon^2}\log\frac{1}{\delta}\right)$ over the sample complexity of predicting the single-district winner under $r$. We further extend our algorithm for the case when the margin of victory is unknown, but we have only two candidates. We then consider the median voting rule when the set of preferences in each district is single-peaked. We show that the winner of a district-based election can be predicted with $\mathcal{O}\left(\frac{1}{\varepsilon^4}\log\frac{1}{\varepsilon}\log\frac{1}{\delta}\right)$ samples even when the harmonious order in different districts can be different and even unknown. Finally, we also show some results for estimating the margin of victory of a district-based election within both additive and multiplicative error bounds.

Approximation Algorithms for ROUND-UFP and ROUND-SAP

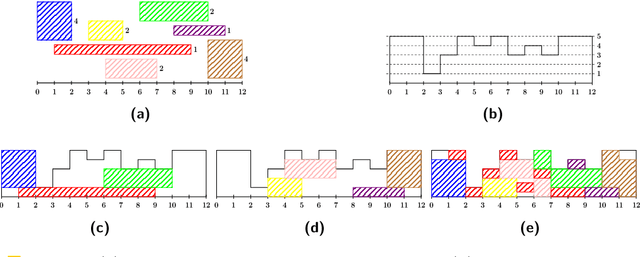
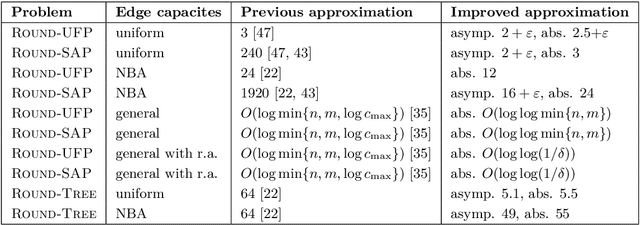
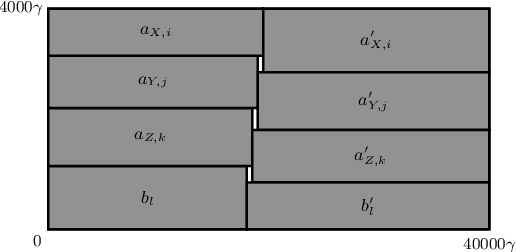
We study ROUND-UFP and ROUND-SAP, two generalizations of the classical BIN PACKING problem that correspond to the unsplittable flow problem on a path (UFP) and the storage allocation problem (SAP), respectively. We are given a path with capacities on its edges and a set of tasks where for each task we are given a demand and a subpath. In ROUND-UFP, the goal is to find a packing of all tasks into a minimum number of copies (rounds) of the given path such that for each copy, the total demand of tasks on any edge does not exceed the capacity of the respective edge. In ROUND-SAP, the tasks are considered to be rectangles and the goal is to find a non-overlapping packing of these rectangles into a minimum number of rounds such that all rectangles lie completely below the capacity profile of the edges. We show that in contrast to BIN PACKING, both the problems do not admit an asymptotic polynomial-time approximation scheme (APTAS), even when all edge capacities are equal. However, for this setting, we obtain asymptotic $(2+\varepsilon)$-approximations for both problems. For the general case, we obtain an $O(\log\log n)$-approximation algorithm and an $O(\log\log\frac{1}{\delta})$-approximation under $(1+\delta)$-resource augmentation for both problems. For the intermediate setting of the no bottleneck assumption (i.e., the maximum task demand is at most the minimum edge capacity), we obtain absolute $12$- and asymptotic $(16+\varepsilon)$-approximation algorithms for ROUND-UFP and ROUND-SAP, respectively.

Feature-based Individual Fairness in k-Clustering

Ensuring fairness in machine learning algorithms is a challenging and important task. We consider the problem of clustering a set of points while ensuring fairness constraints. While there have been several attempts to capture group fairness in the k-clustering problem, fairness at an individual level is not well-studied. We introduce a new notion of individual fairness in k-clustering based on features that are not necessarily used for clustering. We show that this problem is NP-hard and does not admit a constant factor approximation. We then design a randomized algorithm that guarantees approximation both in terms of minimizing the clustering distance objective as well as individual fairness under natural restrictions on the distance metric and fairness constraints. Finally, our experimental results validate that our algorithm produces lower clustering costs compared to existing algorithms while being competitive in individual fairness.