Preference Elicitation For Single Crossing Domain
Paper and Code
Apr 15, 2016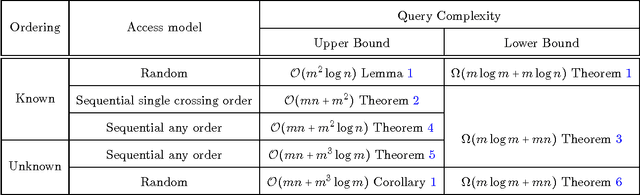
Eliciting the preferences of a set of agents over a set of alternatives is a problem of fundamental importance in social choice theory. Prior work on this problem has studied the query complexity of preference elicitation for the unrestricted domain and for the domain of single peaked preferences. In this paper, we consider the domain of single crossing preference profiles and study the query complexity of preference elicitation under various settings. We consider two distinct situations: when an ordering of the voters with respect to which the profile is single crossing is known versus when it is unknown. We also consider different access models: when the votes can be accessed at random, as opposed to when they are coming in a pre-defined sequence. In the sequential access model, we distinguish two cases when the ordering is known: the first is that sequence in which the votes appear is also a single-crossing order, versus when it is not. The main contribution of our work is to provide polynomial time algorithms with low query complexity for preference elicitation in all the above six cases. Further, we show that the query complexities of our algorithms are optimal up to constant factors for all but one of the above six cases. We then present preference elicitation algorithms for profiles which are close to being single crossing under various notions of closeness, for example, single crossing width, minimum number of candidates | voters whose deletion makes a profile single crossing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge