Fair Division with Market Values

We introduce a model of fair division with market values, where indivisible goods must be partitioned among agents with (additive) subjective valuations, and each good additionally has a market value. The market valuation can be viewed as a separate additive valuation that holds identically across all the agents. We seek allocations that are simultaneously fair with respect to the subjective valuations and with respect to the market valuation. We show that an allocation that satisfies stochastically-dominant envy-freeness up to one good (SD-EF1) with respect to both the subjective valuations and the market valuation does not always exist, but the weaker guarantee of EF1 with respect to the subjective valuations along with SD-EF1 with respect to the market valuation can be guaranteed. We also study a number of other guarantees such as Pareto optimality, EFX, and MMS. In addition, we explore non-additive valuations and extend our model to cake-cutting. Along the way, we identify several tantalizing open questions.

Causal Contextual Bandits with Adaptive Context

We study a variant of causal contextual bandits where the context is chosen based on an initial intervention chosen by the learner. At the beginning of each round, the learner selects an initial action, depending on which a stochastic context is revealed by the environment. Following this, the learner then selects a final action and receives a reward. Given $T$ rounds of interactions with the environment, the objective of the learner is to learn a policy (of selecting the initial and the final action) with maximum expected reward. In this paper we study the specific situation where every action corresponds to intervening on a node in some known causal graph. We extend prior work from the deterministic context setting to obtain simple regret minimization guarantees. This is achieved through an instance-dependent causal parameter, $\lambda$, which characterizes our upper bound. Furthermore, we prove that our simple regret is essentially tight for a large class of instances. A key feature of our work is that we use convex optimization to address the bandit exploration problem. We also conduct experiments to validate our theoretical results, and release our code at our project GitHub repository: https://github.com/adaptiveContextualCausalBandits/aCCB.

Optimal Regret with Limited Adaptivity for Generalized Linear Contextual Bandits

We study the generalized linear contextual bandit problem within the requirements of limited adaptivity. In this paper, we present two algorithms, B-GLinCB and RS-GLinCB, that address, respectively, two prevalent limited adaptivity models: batch learning with stochastic contexts and rare policy switches with adversarial contexts. For both these models, we establish essentially tight regret bounds. Notably, in the obtained bounds, we manage to eliminate a dependence on a key parameter $\kappa$, which captures the non-linearity of the underlying reward model. For our batch learning algorithm B-GLinCB, with $\Omega\left( \log{\log T} \right)$ batches, the regret scales as $\tilde{O}(\sqrt{T})$. Further, we establish that our rarely switching algorithm RS-GLinCB updates its policy at most $\tilde{O}(\log^2 T)$ times and achieves a regret of $\tilde{O}(\sqrt{T})$. Our approach for removing the dependence on $\kappa$ for generalized linear contextual bandits might be of independent interest.

Nash Regret Guarantees for Linear Bandits

We obtain essentially tight upper bounds for a strengthened notion of regret in the stochastic linear bandits framework. The strengthening -- referred to as Nash regret -- is defined as the difference between the (a priori unknown) optimum and the geometric mean of expected rewards accumulated by the linear bandit algorithm. Since the geometric mean corresponds to the well-studied Nash social welfare (NSW) function, this formulation quantifies the performance of a bandit algorithm as the collective welfare it generates across rounds. NSW is known to satisfy fairness axioms and, hence, an upper bound on Nash regret provides a principled fairness guarantee. We consider the stochastic linear bandits problem over a horizon of $T$ rounds and with set of arms ${X}$ in ambient dimension $d$. Furthermore, we focus on settings in which the stochastic reward -- associated with each arm in ${X}$ -- is a non-negative, $\nu$-sub-Poisson random variable. For this setting, we develop an algorithm that achieves a Nash regret of $O\left( \sqrt{\frac{d\nu}{T}} \log( T |X|)\right)$. In addition, addressing linear bandit instances in which the set of arms ${X}$ is not necessarily finite, we obtain a Nash regret upper bound of $O\left( \frac{d^\frac{5}{4}\nu^{\frac{1}{2}}}{\sqrt{T}} \log(T)\right)$. Since bounded random variables are sub-Poisson, these results hold for bounded, positive rewards. Our linear bandit algorithm is built upon the successive elimination method with novel technical insights, including tailored concentration bounds and the use of sampling via John ellipsoid in conjunction with the Kiefer-Wolfowitz optimal design.

Learning Good Interventions in Causal Graphs via Covering

We study the causal bandit problem that entails identifying a near-optimal intervention from a specified set $A$ of (possibly non-atomic) interventions over a given causal graph. Here, an optimal intervention in ${A}$ is one that maximizes the expected value for a designated reward variable in the graph, and we use the standard notion of simple regret to quantify near optimality. Considering Bernoulli random variables and for causal graphs on $N$ vertices with constant in-degree, prior work has achieved a worst case guarantee of $\widetilde{O} (N/\sqrt{T})$ for simple regret. The current work utilizes the idea of covering interventions (which are not necessarily contained within ${A}$) and establishes a simple regret guarantee of $\widetilde{O}(\sqrt{N/T})$. Notably, and in contrast to prior work, our simple regret bound depends only on explicit parameters of the problem instance. We also go beyond prior work and achieve a simple regret guarantee for causal graphs with unobserved variables. Further, we perform experiments to show improvements over baselines in this setting.

Fairness and Welfare Quantification for Regret in Multi-Armed Bandits

We extend the notion of regret with a welfarist perspective. Focussing on the classic multi-armed bandit (MAB) framework, the current work quantifies the performance of bandit algorithms by applying a fundamental welfare function, namely the Nash social welfare (NSW) function. This corresponds to equating algorithm's performance to the geometric mean of its expected rewards and leads us to the study of Nash regret, defined as the difference between the -- a priori unknown -- optimal mean (among the arms) and the algorithm's performance. Since NSW is known to satisfy fairness axioms, our approach complements the utilitarian considerations of average (cumulative) regret, wherein the algorithm is evaluated via the arithmetic mean of its expected rewards. This work develops an algorithm that, given the horizon of play $T$, achieves a Nash regret of $O \left( \sqrt{\frac{{k \log T}}{T}} \right)$, here $k$ denotes the number of arms in the MAB instance. Since, for any algorithm, the Nash regret is at least as much as its average regret (the AM-GM inequality), the known lower bound on average regret holds for Nash regret as well. Therefore, our Nash regret guarantee is essentially tight. In addition, we develop an anytime algorithm with a Nash regret guarantee of $O \left( \sqrt{\frac{{k\log T}}{T}} \log T \right)$.

Intervention Efficient Algorithm for Two-Stage Causal MDPs

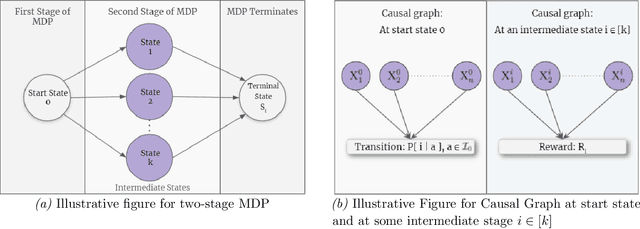
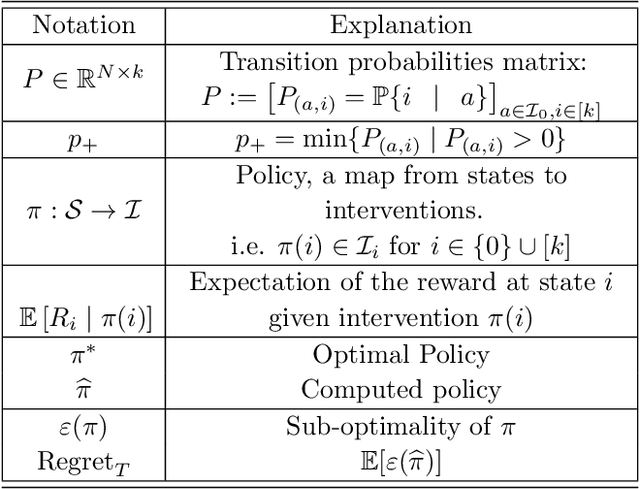
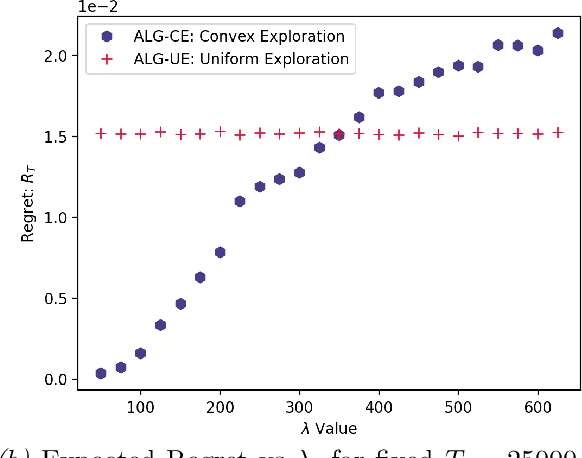
We study Markov Decision Processes (MDP) wherein states correspond to causal graphs that stochastically generate rewards. In this setup, the learner's goal is to identify atomic interventions that lead to high rewards by intervening on variables at each state. Generalizing the recent causal-bandit framework, the current work develops (simple) regret minimization guarantees for two-stage causal MDPs, with parallel causal graph at each state. We propose an algorithm that achieves an instance dependent regret bound. A key feature of our algorithm is that it utilizes convex optimization to address the exploration problem. We identify classes of instances wherein our regret guarantee is essentially tight, and experimentally validate our theoretical results.

Optimal Algorithms for Range Searching over Multi-Armed Bandits

This paper studies a multi-armed bandit (MAB) version of the range-searching problem. In its basic form, range searching considers as input a set of points (on the real line) and a collection of (real) intervals. Here, with each specified point, we have an associated weight, and the problem objective is to find a maximum-weight point within every given interval. The current work addresses range searching with stochastic weights: each point corresponds to an arm (that admits sample access) and the point's weight is the (unknown) mean of the underlying distribution. In this MAB setup, we develop sample-efficient algorithms that find, with high probability, near-optimal arms within the given intervals, i.e., we obtain PAC (probably approximately correct) guarantees. We also provide an algorithm for a generalization wherein the weight of each point is a multi-dimensional vector. The sample complexities of our algorithms depend, in particular, on the size of the optimal hitting set of the given intervals. Finally, we establish lower bounds proving that the obtained sample complexities are essentially tight. Our results highlight the significance of geometric constructs -- specifically, hitting sets -- in our MAB setting.

Quantifying Infra-Marginality and Its Trade-off with Group Fairness

In critical decision-making scenarios, optimizing accuracy can lead to a biased classifier, hence past work recommends enforcing group-based fairness metrics in addition to maximizing accuracy. However, doing so exposes the classifier to another kind of bias called infra-marginality. This refers to individual-level bias where some individuals/subgroups can be worse off than under simply optimizing for accuracy. For instance, a classifier implementing race-based parity may significantly disadvantage women of the advantaged race. To quantify this bias, we propose a general notion of $\eta$-infra-marginality that can be used to evaluate the extent of this bias. We prove theoretically that, unlike other fairness metrics, infra-marginality does not have a trade-off with accuracy: high accuracy directly leads to low infra-marginality. This observation is confirmed through empirical analysis on multiple simulated and real-world datasets. Further, we find that maximizing group fairness often increases infra-marginality, suggesting the consideration of both group-level fairness and individual-level infra-marginality. However, measuring infra-marginality requires knowledge of the true distribution of individual-level outcomes correctly and explicitly. We propose a practical method to measure infra-marginality, and a simple algorithm to maximize group-wise accuracy and avoid infra-marginality.

Fair Division Under Cardinality Constraints

We consider the problem of fairly allocating indivisible goods, among agents, under cardinality constraints and additive valuations. In this setting, we are given a partition of the entire set of goods---i.e., the goods are categorized---and a limit is specified on the number of goods that can be allocated from each category to any agent. The objective here is to find a fair allocation in which the subset of goods assigned to any agent satisfies the given cardinality constraints. This problem naturally captures a number of resource-allocation applications, and is a generalization of the well-studied (unconstrained) fair division problem. The two central notions of fairness, in the context of fair division of indivisible goods, are envy freeness up to one good (EF1) and the (approximate) maximin share guarantee (MMS). We show that the existence and algorithmic guarantees established for these solution concepts in the unconstrained setting can essentially be achieved under cardinality constraints. Specifically, we develop efficient algorithms which compute EF1 and approximately MMS allocations in the constrained setting. Furthermore, focusing on the case wherein all the agents have the same additive valuation, we establish that EF1 allocations exist and can be computed efficiently even under matroid constraints.