SWEPO: Simultaneous Weighted Preference Optimization for Group Contrastive Alignment

We introduce Simultaneous Weighted Preference Optimization (SWEPO), a novel extension of Direct Preference Optimization (DPO) designed to accommodate multiple dynamically chosen positive and negative responses for each query. SWEPO employs a weighted group contrastive loss, assigning weights to responses based on their deviation from the mean reward score. This approach effectively prioritizes responses that are significantly better or worse than the average, enhancing optimization. Our theoretical analysis demonstrates that simultaneously considering multiple preferences reduces alignment bias, resulting in more robust alignment. Additionally, we provide insights into the training dynamics of our loss function and a related function, InfoNCA. Empirical validation on the UltraFeedback dataset establishes SWEPO as state-of-the-art, with superior performance in downstream evaluations using the AlpacaEval dataset.

Time-Reversal Provides Unsupervised Feedback to LLMs

Large Language Models (LLMs) are typically trained to predict in the forward direction of time. However, recent works have shown that prompting these models to look back and critique their own generations can produce useful feedback. Motivated by this, we explore the question of whether LLMs can be empowered to think (predict and score) backwards to provide unsupervised feedback that complements forward LLMs. Towards this, we introduce Time Reversed Language Models (TRLMs), which can score and generate queries when conditioned on responses, effectively functioning in the reverse direction of time. Further, to effectively infer in the response to query direction, we pre-train and fine-tune a language model (TRLM-Ba) in the reverse token order from scratch. We show empirically (and theoretically in a stylized setting) that time-reversed models can indeed complement forward model predictions when used to score the query given response for re-ranking multiple forward generations. We obtain up to 5\% improvement on the widely used AlpacaEval Leaderboard over the competent baseline of best-of-N re-ranking using self log-perplexity scores. We further show that TRLM scoring outperforms conventional forward scoring of response given query, resulting in significant gains in applications such as citation generation and passage retrieval. We next leverage the generative ability of TRLM to augment or provide unsupervised feedback to input safety filters of LLMs, demonstrating a drastic reduction in false negative rate with negligible impact on false positive rates against several attacks published on the popular JailbreakBench leaderboard.

Causal Contextual Bandits with Adaptive Context

We study a variant of causal contextual bandits where the context is chosen based on an initial intervention chosen by the learner. At the beginning of each round, the learner selects an initial action, depending on which a stochastic context is revealed by the environment. Following this, the learner then selects a final action and receives a reward. Given $T$ rounds of interactions with the environment, the objective of the learner is to learn a policy (of selecting the initial and the final action) with maximum expected reward. In this paper we study the specific situation where every action corresponds to intervening on a node in some known causal graph. We extend prior work from the deterministic context setting to obtain simple regret minimization guarantees. This is achieved through an instance-dependent causal parameter, $\lambda$, which characterizes our upper bound. Furthermore, we prove that our simple regret is essentially tight for a large class of instances. A key feature of our work is that we use convex optimization to address the bandit exploration problem. We also conduct experiments to validate our theoretical results, and release our code at our project GitHub repository: https://github.com/adaptiveContextualCausalBandits/aCCB.

Causal ATE Mitigates Unintended Bias in Controlled Text Generation

We study attribute control in language models through the method of Causal Average Treatment Effect (Causal ATE). Existing methods for the attribute control task in Language Models (LMs) check for the co-occurrence of words in a sentence with the attribute of interest, and control for them. However, spurious correlation of the words with the attribute in the training dataset, can cause models to hallucinate the presence of the attribute when presented with the spurious correlate during inference. We show that the simple perturbation-based method of Causal ATE removes this unintended effect. Additionally, we offer a theoretical foundation for investigating Causal ATE in the classification task, and prove that it reduces the number of false positives -- thereby mitigating the issue of unintended bias. Specifically, we ground it in the problem of toxicity mitigation, where a significant challenge lies in the inadvertent bias that often emerges towards protected groups post detoxification. We show that this unintended bias can be solved by the use of the Causal ATE metric.

CFL: Causally Fair Language Models Through Token-level Attribute Controlled Generation

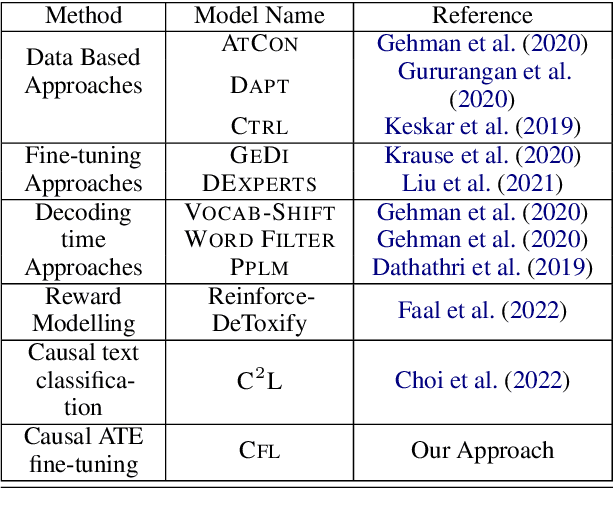
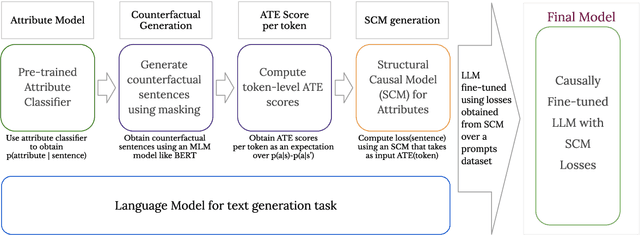
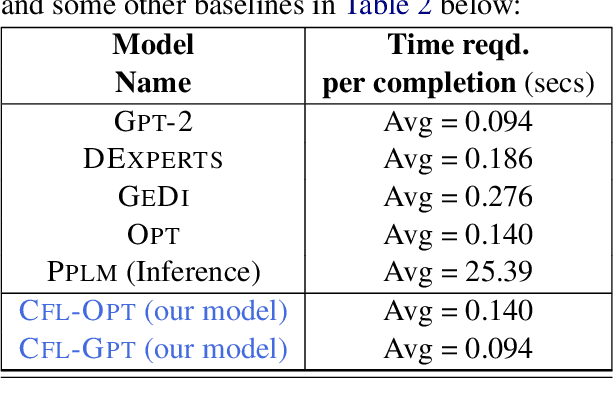
We propose a method to control the attributes of Language Models (LMs) for the text generation task using Causal Average Treatment Effect (ATE) scores and counterfactual augmentation. We explore this method, in the context of LM detoxification, and propose the Causally Fair Language (CFL) architecture for detoxifying pre-trained LMs in a plug-and-play manner. Our architecture is based on a Structural Causal Model (SCM) that is mathematically transparent and computationally efficient as compared with many existing detoxification techniques. We also propose several new metrics that aim to better understand the behaviour of LMs in the context of toxic text generation. Further, we achieve state of the art performance for toxic degeneration, which are computed using \RTP (RTP) benchmark. Our experiments show that CFL achieves such a detoxification without much impact on the model perplexity. We also show that CFL mitigates the unintended bias problem through experiments on the BOLD dataset.

Learning Good Interventions in Causal Graphs via Covering

We study the causal bandit problem that entails identifying a near-optimal intervention from a specified set $A$ of (possibly non-atomic) interventions over a given causal graph. Here, an optimal intervention in ${A}$ is one that maximizes the expected value for a designated reward variable in the graph, and we use the standard notion of simple regret to quantify near optimality. Considering Bernoulli random variables and for causal graphs on $N$ vertices with constant in-degree, prior work has achieved a worst case guarantee of $\widetilde{O} (N/\sqrt{T})$ for simple regret. The current work utilizes the idea of covering interventions (which are not necessarily contained within ${A}$) and establishes a simple regret guarantee of $\widetilde{O}(\sqrt{N/T})$. Notably, and in contrast to prior work, our simple regret bound depends only on explicit parameters of the problem instance. We also go beyond prior work and achieve a simple regret guarantee for causal graphs with unobserved variables. Further, we perform experiments to show improvements over baselines in this setting.

Intervention Efficient Algorithm for Two-Stage Causal MDPs

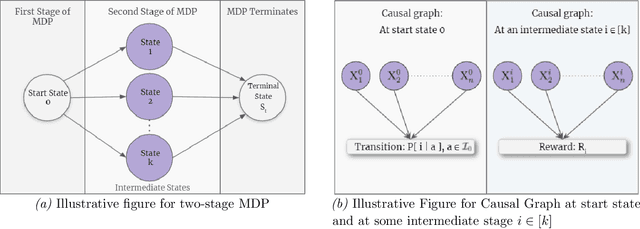
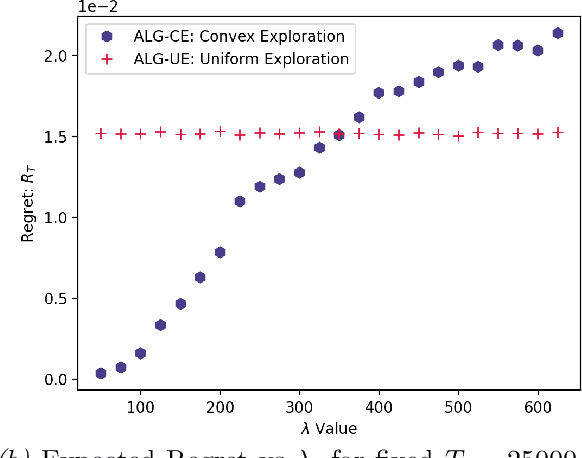
We study Markov Decision Processes (MDP) wherein states correspond to causal graphs that stochastically generate rewards. In this setup, the learner's goal is to identify atomic interventions that lead to high rewards by intervening on variables at each state. Generalizing the recent causal-bandit framework, the current work develops (simple) regret minimization guarantees for two-stage causal MDPs, with parallel causal graph at each state. We propose an algorithm that achieves an instance dependent regret bound. A key feature of our algorithm is that it utilizes convex optimization to address the exploration problem. We identify classes of instances wherein our regret guarantee is essentially tight, and experimentally validate our theoretical results.

Scale Invariant Solutions for Overdetermined Linear Systems with Applications to Reinforcement Learning

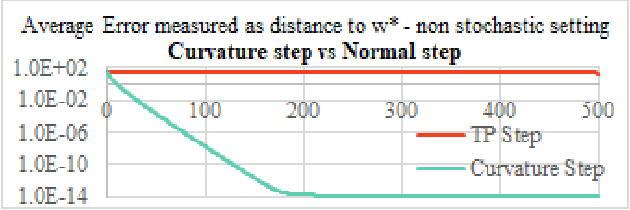
Overdetermined linear systems are common in reinforcement learning, e.g., in Q and value function estimation with function approximation. The standard least-squares criterion, however, leads to a solution that is unduly influenced by rows with large norms. This is a serious issue, especially when the matrices in these systems are beyond user control. To address this, we propose a scale-invariant criterion that we then use to develop two novel algorithms for value function estimation: Normalized Monte Carlo and Normalized TD(0). Separately, we also introduce a novel adaptive stepsize that may be useful beyond this work as well. We use simulations and theoretical guarantees to demonstrate the efficacy of our ideas.