Scale Invariant Solutions for Overdetermined Linear Systems with Applications to Reinforcement Learning
Paper and Code
Apr 15, 2021
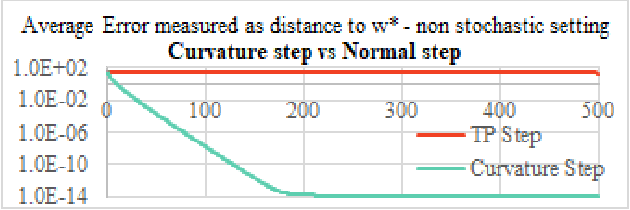

Overdetermined linear systems are common in reinforcement learning, e.g., in Q and value function estimation with function approximation. The standard least-squares criterion, however, leads to a solution that is unduly influenced by rows with large norms. This is a serious issue, especially when the matrices in these systems are beyond user control. To address this, we propose a scale-invariant criterion that we then use to develop two novel algorithms for value function estimation: Normalized Monte Carlo and Normalized TD(0). Separately, we also introduce a novel adaptive stepsize that may be useful beyond this work as well. We use simulations and theoretical guarantees to demonstrate the efficacy of our ideas.
* 53 pages, 12 figures (9 pages main body with 5 figures)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge