Intervention Efficient Algorithm for Two-Stage Causal MDPs
Paper and Code
Nov 01, 2021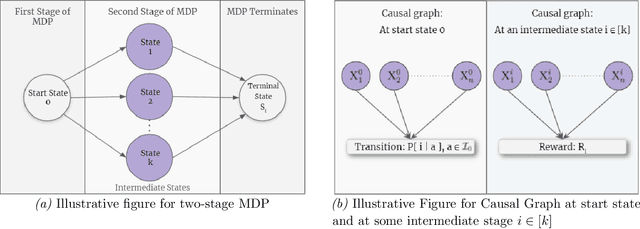
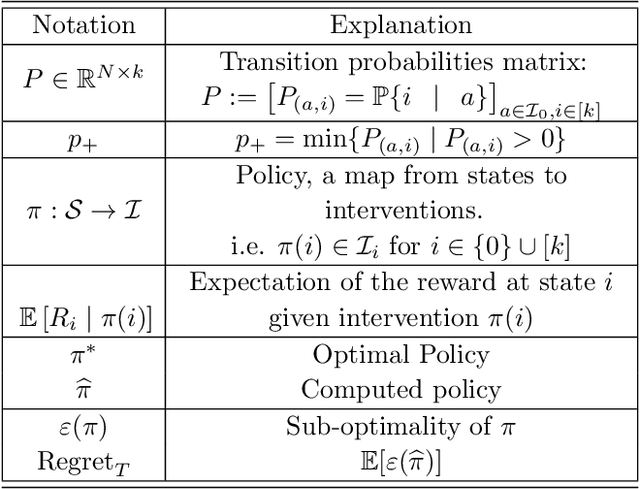
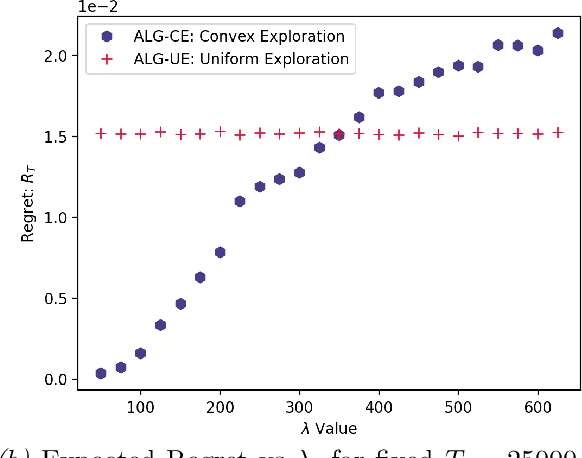
We study Markov Decision Processes (MDP) wherein states correspond to causal graphs that stochastically generate rewards. In this setup, the learner's goal is to identify atomic interventions that lead to high rewards by intervening on variables at each state. Generalizing the recent causal-bandit framework, the current work develops (simple) regret minimization guarantees for two-stage causal MDPs, with parallel causal graph at each state. We propose an algorithm that achieves an instance dependent regret bound. A key feature of our algorithm is that it utilizes convex optimization to address the exploration problem. We identify classes of instances wherein our regret guarantee is essentially tight, and experimentally validate our theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge