Proportional Fairness in Non-Centroid Clustering

We revisit the recently developed framework of proportionally fair clustering, where the goal is to provide group fairness guarantees that become stronger for groups of data points (agents) that are large and cohesive. Prior work applies this framework to centroid clustering, where the loss of an agent is its distance to the centroid assigned to its cluster. We expand the framework to non-centroid clustering, where the loss of an agent is a function of the other agents in its cluster, by adapting two proportional fairness criteria -- the core and its relaxation, fully justified representation (FJR) -- to this setting. We show that the core can be approximated only under structured loss functions, and even then, the best approximation we are able to establish, using an adaptation of the GreedyCapture algorithm developed for centroid clustering [Chen et al., 2019; Micha and Shah, 2020], is unappealing for a natural loss function. In contrast, we design a new (inefficient) algorithm, GreedyCohesiveClustering, which achieves the relaxation FJR exactly under arbitrary loss functions, and show that the efficient GreedyCapture algorithm achieves a constant approximation of FJR. We also design an efficient auditing algorithm, which estimates the FJR approximation of any given clustering solution up to a constant factor. Our experiments on real data suggest that traditional clustering algorithms are highly unfair, whereas GreedyCapture is considerably fairer and incurs only a modest loss in common clustering objectives.

Fair Division with Market Values

We introduce a model of fair division with market values, where indivisible goods must be partitioned among agents with (additive) subjective valuations, and each good additionally has a market value. The market valuation can be viewed as a separate additive valuation that holds identically across all the agents. We seek allocations that are simultaneously fair with respect to the subjective valuations and with respect to the market valuation. We show that an allocation that satisfies stochastically-dominant envy-freeness up to one good (SD-EF1) with respect to both the subjective valuations and the market valuation does not always exist, but the weaker guarantee of EF1 with respect to the subjective valuations along with SD-EF1 with respect to the market valuation can be guaranteed. We also study a number of other guarantees such as Pareto optimality, EFX, and MMS. In addition, we explore non-additive valuations and extend our model to cake-cutting. Along the way, we identify several tantalizing open questions.

Group Fairness in Peer Review

Large conferences such as NeurIPS and AAAI serve as crossroads of various AI fields, since they attract submissions from a vast number of communities. However, in some cases, this has resulted in a poor reviewing experience for some communities, whose submissions get assigned to less qualified reviewers outside of their communities. An often-advocated solution is to break up any such large conference into smaller conferences, but this can lead to isolation of communities and harm interdisciplinary research. We tackle this challenge by introducing a notion of group fairness, called the core, which requires that every possible community (subset of researchers) to be treated in a way that prevents them from unilaterally benefiting by withdrawing from a large conference. We study a simple peer review model, prove that it always admits a reviewing assignment in the core, and design an efficient algorithm to find one such assignment. We use real data from CVPR and ICLR conferences to compare our algorithm to existing reviewing assignment algorithms on a number of metrics.

Harm Ratio: A Novel and Versatile Fairness Criterion

Envy-freeness has become the cornerstone of fair division research. In settings where each individual is allocated a disjoint share of collective resources, it is a compelling fairness axiom which demands that no individual strictly prefer the allocation of another individual to their own. Unfortunately, in many real-life collective decision-making problems, the goal is to choose a (common) public outcome that is equally applicable to all individuals, and the notion of envy becomes vacuous. Consequently, this literature has avoided studying fairness criteria that focus on individuals feeling a sense of jealousy or resentment towards other individuals (rather than towards the system), missing out on a key aspect of fairness. In this work, we propose a novel fairness criterion, individual harm ratio, which is inspired by envy-freeness but applies to a broad range of collective decision-making settings. Theoretically, we identify minimal conditions under which this criterion and its groupwise extensions can be guaranteed, and study the computational complexity of related problems. Empirically, we conduct experiments with real data to show that our fairness criterion is powerful enough to differentiate between prominent decision-making algorithms for a range of tasks from voting and fair division to participatory budgeting and peer review.

Best of Both Distortion Worlds

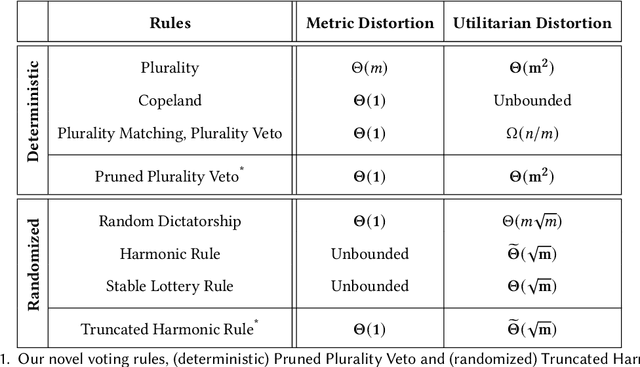
We study the problem of designing voting rules that take as input the ordinal preferences of $n$ agents over a set of $m$ alternatives and output a single alternative, aiming to optimize the overall happiness of the agents. The input to the voting rule is each agent's ranking of the alternatives from most to least preferred, yet the agents have more refined (cardinal) preferences that capture the intensity with which they prefer one alternative over another. To quantify the extent to which voting rules can optimize over the cardinal preferences given access only to the ordinal ones, prior work has used the distortion measure, i.e., the worst-case approximation ratio between a voting rule's performance and the best performance achievable given the cardinal preferences. The work on the distortion of voting rules has been largely divided into two worlds: utilitarian distortion and metric distortion. In the former, the cardinal preferences of the agents correspond to general utilities and the goal is to maximize a normalized social welfare. In the latter, the agents' cardinal preferences correspond to costs given by distances in an underlying metric space and the goal is to minimize the (unnormalized) social cost. Several deterministic and randomized voting rules have been proposed and evaluated for each of these worlds separately, gradually improving the achievable distortion bounds, but none of the known voting rules perform well in both worlds simultaneously. In this work, we prove that one can achieve the best of both worlds by designing new voting rules, that simultaneously achieve near-optimal distortion guarantees in both distortion worlds. We also prove that this positive result does not generalize to the case where the voting rule is provided with the rankings of only the top-$t$ alternatives of each agent, for $t<m$.

How Far Can I Go ? : A Self-Supervised Approach for Deterministic Video Depth Forecasting

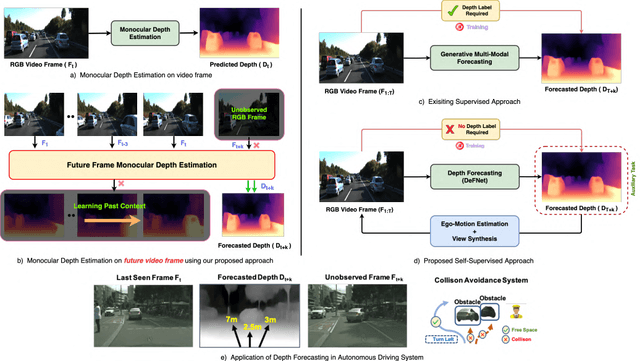
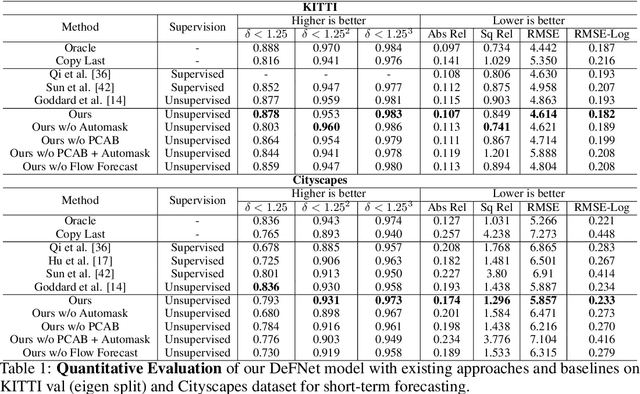
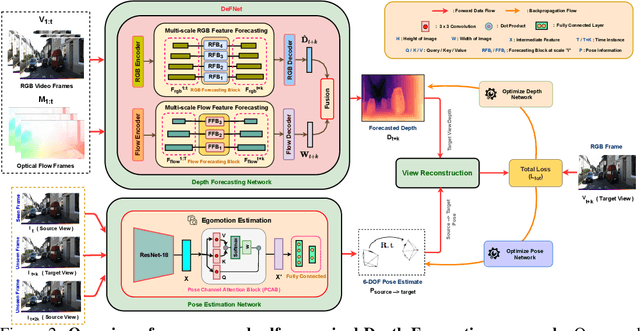
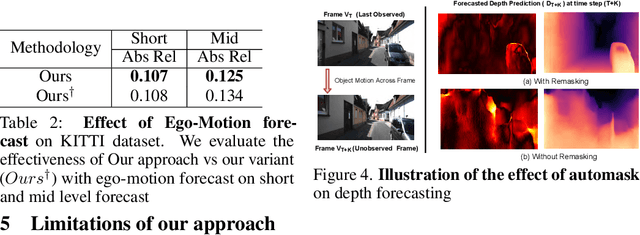
In this paper we present a novel self-supervised method to anticipate the depth estimate for a future, unobserved real-world urban scene. This work is the first to explore self-supervised learning for estimation of monocular depth of future unobserved frames of a video. Existing works rely on a large number of annotated samples to generate the probabilistic prediction of depth for unseen frames. However, this makes it unrealistic due to its requirement for large amount of annotated depth samples of video. In addition, the probabilistic nature of the case, where one past can have multiple future outcomes often leads to incorrect depth estimates. Unlike previous methods, we model the depth estimation of the unobserved frame as a view-synthesis problem, which treats the depth estimate of the unseen video frame as an auxiliary task while synthesizing back the views using learned pose. This approach is not only cost effective - we do not use any ground truth depth for training (hence practical) but also deterministic (a sequence of past frames map to an immediate future). To address this task we first develop a novel depth forecasting network DeFNet which estimates depth of unobserved future by forecasting latent features. Second, we develop a channel-attention based pose estimation network that estimates the pose of the unobserved frame. Using this learned pose, estimated depth map is reconstructed back into the image domain, thus forming a self-supervised solution. Our proposed approach shows significant improvements in Abs Rel metric compared to state-of-the-art alternatives on both short and mid-term forecasting setting, benchmarked on KITTI and Cityscapes. Code is available at https://github.com/sauradip/depthForecasting

Two-Sided Matching Meets Fair Division

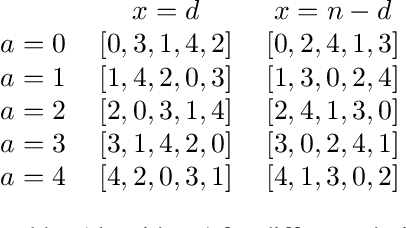
We introduce a new model for two-sided matching which allows us to borrow popular fairness notions from the fair division literature such as envy-freeness up to one good and maximin share guarantee. In our model, each agent is matched to multiple agents on the other side over whom she has additive preferences. We demand fairness for each side separately, giving rise to notions such as double envy-freeness up to one match (DEF1) and double maximin share guarantee (DMMS). We show that (a slight strengthening of) DEF1 cannot always be achieved, but in the special case where both sides have identical preferences, the round-robin algorithm with a carefully designed agent ordering achieves it. In contrast, DMMS cannot be achieved even when both sides have identical preferences.

Fair and Efficient Resource Allocation with Partial Information

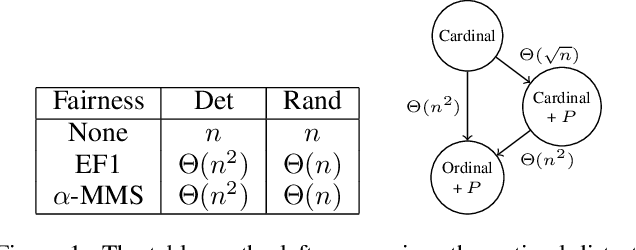
We study the fundamental problem of allocating indivisible goods to agents with additive preferences. We consider eliciting from each agent only a ranking of her $k$ most preferred goods instead of her full cardinal valuations. We characterize the value of $k$ needed to achieve envy-freeness up to one good and approximate maximin share guarantee, two widely studied fairness notions. We also analyze the multiplicative loss in social welfare incurred due to the lack of full information with and without the fairness requirements.

Surprisingly Popular Voting Recovers Rankings, Surprisingly!

The wisdom of the crowd has long become the de facto approach for eliciting information from individuals or experts in order to predict the ground truth. However, classical democratic approaches for aggregating individual \emph{votes} only work when the opinion of the majority of the crowd is relatively accurate. A clever recent approach, \emph{surprisingly popular voting}, elicits additional information from the individuals, namely their \emph{prediction} of other individuals' votes, and provably recovers the ground truth even when experts are in minority. This approach works well when the goal is to pick the correct option from a small list, but when the goal is to recover a true ranking of the alternatives, a direct application of the approach requires eliciting too much information. We explore practical techniques for extending the surprisingly popular algorithm to ranked voting by partial votes and predictions and designing robust aggregation rules. We experimentally demonstrate that even a little prediction information helps surprisingly popular voting outperform classical approaches.

Learning Desirable Matchings From Partial Preferences

We study the classic problem of matching $n$ agents to $n$ objects, where the agents have ranked preferences over the objects. We focus on two popular desiderata from the matching literature: Pareto optimality and rank-maximality. Instead of asking the agents to report their complete preferences, our goal is to learn a desirable matching from partial preferences, specifically a matching that is necessarily Pareto optimal (NPO) or necessarily rank-maximal (NRM) under any completion of the partial preferences. We focus on the top-$k$ model in which agents reveal a prefix of their preference rankings. We design efficient algorithms to check if a given matching is NPO or NRM, and to check whether such a matching exists given top-$k$ partial preferences. We also study online algorithms to elicit partial preferences adaptively, and prove bounds on their competitive ratio.