Matching Markets Meet LLMs: Algorithmic Reasoning with Ranked Preferences

The rise of Large Language Models (LLMs) has driven progress in reasoning tasks -- from program synthesis to scientific hypothesis generation -- yet their ability to handle ranked preferences and structured algorithms in combinatorial domains remains underexplored. We study matching markets, a core framework behind applications like resource allocation and ride-sharing, which require reconciling individual ranked preferences to ensure stable outcomes. We evaluate several state-of-the-art models on a hierarchy of preference-based reasoning tasks -- ranging from stable-matching generation to instability detection, instability resolution, and fine-grained preference queries -- to systematically expose their logical and algorithmic limitations in handling ranked inputs. Surprisingly, even top-performing models with advanced reasoning struggle to resolve instability in large markets, often failing to identify blocking pairs or execute algorithms iteratively. We further show that parameter-efficient fine-tuning (LoRA) significantly improves performance in small markets, but fails to bring about a similar improvement on large instances, suggesting the need for more sophisticated strategies to improve LLMs' reasoning with larger-context inputs.

AI Education in a Mirror: Challenges Faced by Academic and Industry Experts

As Artificial Intelligence (AI) technologies continue to evolve, the gap between academic AI education and real-world industry challenges remains an important area of investigation. This study provides preliminary insights into challenges AI professionals encounter in both academia and industry, based on semi-structured interviews with 14 AI experts - eight from industry and six from academia. We identify key challenges related to data quality and availability, model scalability, practical constraints, user behavior, and explainability. While both groups experience data and model adaptation difficulties, industry professionals more frequently highlight deployment constraints, resource limitations, and external dependencies, whereas academics emphasize theoretical adaptation and standardization issues. These exploratory findings suggest that AI curricula could better integrate real-world complexities, software engineering principles, and interdisciplinary learning, while recognizing the broader educational goals of building foundational and ethical reasoning skills.

Bandit Learning in Matching Markets: Utilitarian and Rawlsian Perspectives

Two-sided matching markets have demonstrated significant impact in many real-world applications, including school choice, medical residency placement, electric vehicle charging, ride sharing, and recommender systems. However, traditional models often assume that preferences are known, which is not always the case in modern markets, where preferences are unknown and must be learned. For example, a company may not know its preference over all job applicants a priori in online markets. Recent research has modeled matching markets as multi-armed bandit (MAB) problem and primarily focused on optimizing matching for one side of the market, while often resulting in a pessimal solution for the other side. In this paper, we adopt a welfarist approach for both sides of the market, focusing on two metrics: (1) Utilitarian welfare and (2) Rawlsian welfare, while maintaining market stability. For these metrics, we propose algorithms based on epoch Explore-Then-Commit (ETC) and analyze their regret bounds. Finally, we conduct simulated experiments to evaluate both welfare and market stability.

Surprisingly Popular Voting for Concentric Rank-Order Models

An important problem on social information sites is the recovery of ground truth from individual reports when the experts are in the minority. The wisdom of the crowd, i.e. the collective opinion of a group of individuals fails in such a scenario. However, the surprisingly popular (SP) algorithm~\cite{prelec2017solution} can recover the ground truth even when the experts are in the minority, by asking the individuals to report additional prediction reports--their beliefs about the reports of others. Several recent works have extended the surprisingly popular algorithm to an equivalent voting rule (SP-voting) to recover the ground truth ranking over a set of $m$ alternatives. However, we are yet to fully understand when SP-voting can recover the ground truth ranking, and if so, how many samples (votes and predictions) it needs. We answer this question by proposing two rank-order models and analyzing the sample complexity of SP-voting under these models. In particular, we propose concentric mixtures of Mallows and Plackett-Luce models with $G (\ge 2)$ groups. Our models generalize previously proposed concentric mixtures of Mallows models with $2$ groups, and we highlight the importance of $G > 2$ groups by identifying three distinct groups (expert, intermediate, and non-expert) from existing datasets. Next, we provide conditions on the parameters of the underlying models so that SP-voting can recover ground-truth rankings with high probability, and also derive sample complexities under the same. We complement the theoretical results by evaluating SP-voting on simulated and real datasets.

Putting Gale & Shapley to Work: Guaranteeing Stability Through Learning

Two-sided matching markets describe a large class of problems wherein participants from one side of the market must be matched to those from the other side according to their preferences. In many real-world applications (e.g. content matching or online labor markets), the knowledge about preferences may not be readily available and must be learned, i.e., one side of the market (aka agents) may not know their preferences over the other side (aka arms). Recent research on online settings has focused primarily on welfare optimization aspects (i.e. minimizing the overall regret) while paying little attention to the game-theoretic properties such as the stability of the final matching. In this paper, we exploit the structure of stable solutions to devise algorithms that improve the likelihood of finding stable solutions. We initiate the study of the sample complexity of finding a stable matching, and provide theoretical bounds on the number of samples needed to reach a stable matching with high probability. Finally, our empirical results demonstrate intriguing tradeoffs between stability and optimality of the proposed algorithms, further complementing our theoretical findings.

The Fairness Fair: Bringing Human Perception into Collective Decision-Making

Fairness is one of the most desirable societal principles in collective decision-making. It has been extensively studied in the past decades for its axiomatic properties and has received substantial attention from the multiagent systems community in recent years for its theoretical and computational aspects in algorithmic decision-making. However, these studies are often not sufficiently rich to capture the intricacies of human perception of fairness in the ambivalent nature of the real-world problems. We argue that not only fair solutions should be deemed desirable by social planners (designers), but they should be governed by human and societal cognition, consider perceived outcomes based on human judgement, and be verifiable. We discuss how achieving this goal requires a broad transdisciplinary approach ranging from computing and AI to behavioral economics and human-AI interaction. In doing so, we identify shortcomings and long-term challenges of the current literature of fair division, describe recent efforts in addressing them, and more importantly, highlight a series of open research directions.

Graphical House Allocation

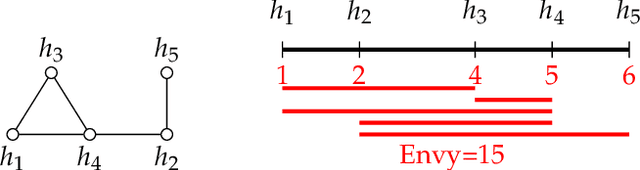
The classical house allocation problem involves assigning $n$ houses (or items) to $n$ agents according to their preferences. A key criterion in such problems is satisfying some fairness constraints such as envy-freeness. We consider a generalization of this problem wherein the agents are placed along the vertices of a graph (corresponding to a social network), and each agent can only experience envy towards its neighbors. Our goal is to minimize the aggregate envy among the agents as a natural fairness objective, i.e., the sum of all pairwise envy values over all edges in a social graph. When agents have identical and evenly-spaced valuations, our problem reduces to the well-studied problem of linear arrangements. For identical valuations with possibly uneven spacing, we show a number of deep and surprising ways in which our setting is a departure from this classical problem. More broadly, we contribute several structural and computational results for various classes of graphs, including NP-hardness results for disjoint unions of paths, cycles, stars, or cliques, and fixed-parameter tractable (and, in some cases, polynomial-time) algorithms for paths, cycles, stars, cliques, and their disjoint unions. Additionally, a conceptual contribution of our work is the formulation of a structural property for disconnected graphs that we call separability which results in efficient parameterized algorithms for finding optimal allocations.

Surprisingly Popular Voting Recovers Rankings, Surprisingly!

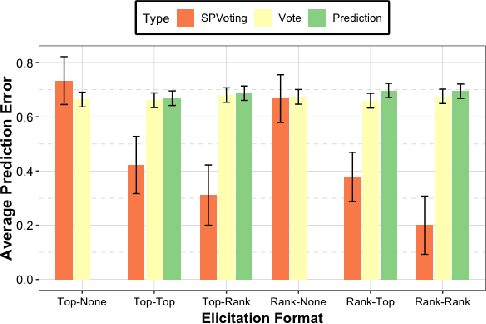
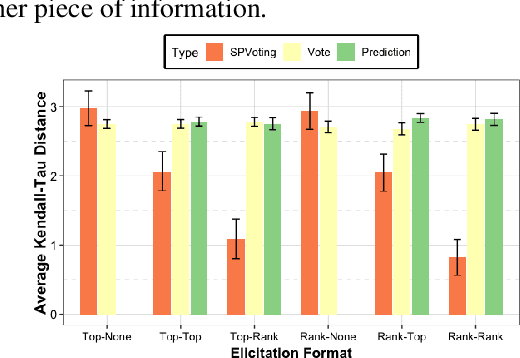
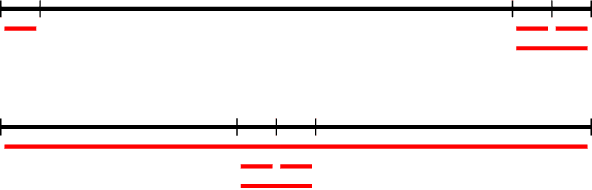
The wisdom of the crowd has long become the de facto approach for eliciting information from individuals or experts in order to predict the ground truth. However, classical democratic approaches for aggregating individual \emph{votes} only work when the opinion of the majority of the crowd is relatively accurate. A clever recent approach, \emph{surprisingly popular voting}, elicits additional information from the individuals, namely their \emph{prediction} of other individuals' votes, and provably recovers the ground truth even when experts are in minority. This approach works well when the goal is to pick the correct option from a small list, but when the goal is to recover a true ranking of the alternatives, a direct application of the approach requires eliciting too much information. We explore practical techniques for extending the surprisingly popular algorithm to ranked voting by partial votes and predictions and designing robust aggregation rules. We experimentally demonstrate that even a little prediction information helps surprisingly popular voting outperform classical approaches.

Guaranteeing Maximin Shares: Some Agents Left Behind

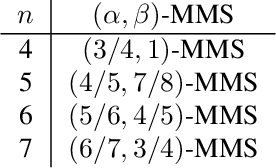
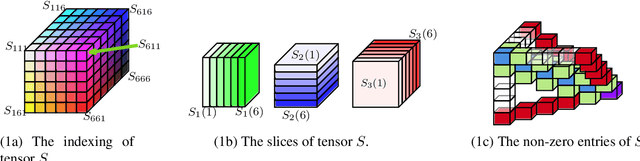
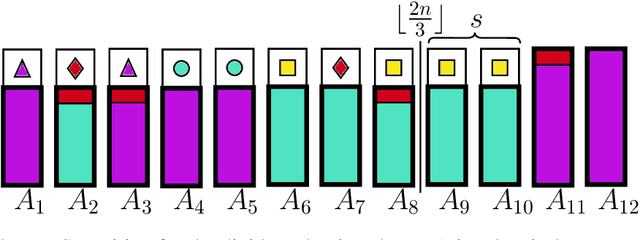
The maximin share (MMS) guarantee is a desirable fairness notion for allocating indivisible goods. While MMS allocations do not always exist, several approximation techniques have been developed to ensure that all agents receive a fraction of their maximin share. We focus on an alternative approximation notion, based on the population of agents, that seeks to guarantee MMS for a fraction of agents. We show that no optimal approximation algorithm can satisfy more than a constant number of agents, and discuss the existence and computation of MMS for all but one agent and its relation to approximate MMS guarantees. We then prove the existence of allocations that guarantee MMS for $\frac{2}{3}$ of agents, and devise a polynomial time algorithm that achieves this bound for up to nine agents. A key implication of our result is the existence of allocations that guarantee $\text{MMS}^{\lceil{3n/2}\rceil}$, i.e., the value that agents receive by partitioning the goods into $\lceil{\frac{3}{2}n}\rceil$ bundles, improving the best known guarantee of $\text{MMS}^{2n-2}$. Finally, we provide empirical experiments using synthetic data.

Learning Desirable Matchings From Partial Preferences

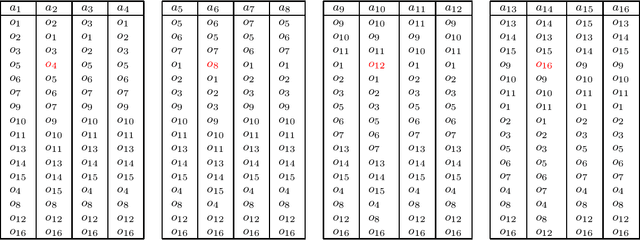
We study the classic problem of matching $n$ agents to $n$ objects, where the agents have ranked preferences over the objects. We focus on two popular desiderata from the matching literature: Pareto optimality and rank-maximality. Instead of asking the agents to report their complete preferences, our goal is to learn a desirable matching from partial preferences, specifically a matching that is necessarily Pareto optimal (NPO) or necessarily rank-maximal (NRM) under any completion of the partial preferences. We focus on the top-$k$ model in which agents reveal a prefix of their preference rankings. We design efficient algorithms to check if a given matching is NPO or NRM, and to check whether such a matching exists given top-$k$ partial preferences. We also study online algorithms to elicit partial preferences adaptively, and prove bounds on their competitive ratio.