Improving Welfare in One-sided Matching using Simple Threshold Queries

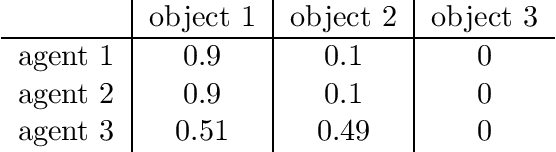
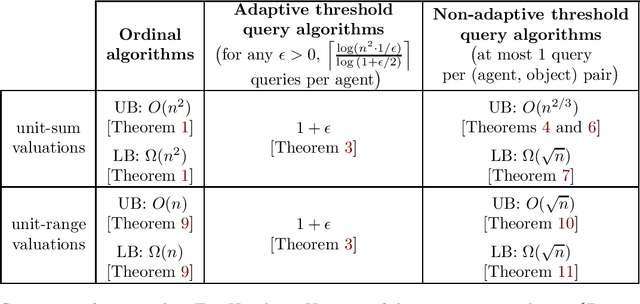
We study one-sided matching problems where $n$ agents have preferences over $m$ objects and each of them need to be assigned to at most one object. Most work on such problems assume that the agents only have ordinal preferences and usually the goal in them is to compute a matching that satisfies some notion of economic efficiency. However, in reality, agents may have some preference intensities or cardinal utilities that, e.g., indicate that they like an an object much more than another object, and not taking these into account can result in a loss in welfare. While one way to potentially account for these is to directly ask the agents for this information, such an elicitation process is cognitively demanding. Therefore, we focus on learning more about their cardinal preferences using simple threshold queries which ask an agent if they value an object greater than a certain value, and use this in turn to come up with algorithms that produce a matching that, for a particular economic notion $X$, satisfies $X$ and also achieves a good approximation to the optimal welfare among all matchings that satisfy $X$. We focus on several notions of economic efficiency, and look at both adaptive and non-adaptive algorithms. Overall, our results show how one can improve welfare by even non-adaptively asking the agents for just one bit of extra information per object.

Algorithmic Stability in Fair Allocation of Indivisible Goods Among Two Agents

We propose a notion of algorithmic stability for scenarios where cardinal preferences are elicited. Informally, our definition captures the idea that an agent should not experience a large change in their utility as long as they make "small" or "innocuous" mistakes while reporting their preferences. We study this notion in the context of fair and efficient allocations of indivisible goods among two agents, and show that it is impossible to achieve exact stability along with even a weak notion of fairness and even approximate efficiency. As a result, we propose two relaxations to stability, namely, approximate-stability and weak-approximate-stability, and show how existing algorithms in the fair division literature that guarantee fair and efficient outcomes perform poorly with respect to these relaxations. This leads us to the explore the possibility of designing new algorithms that are more stable. Towards this end we present a general characterization result for pairwise maximin share allocations, and in turn use it to design an algorithm that is approximately-stable and guarantees a pairwise maximin share and Pareto optimal allocation for two agents. Finally, we present a simple framework that can be used to modify existing fair and efficient algorithms in order to ensure that they also achieve weak-approximate-stability.

Learning Desirable Matchings From Partial Preferences

We study the classic problem of matching $n$ agents to $n$ objects, where the agents have ranked preferences over the objects. We focus on two popular desiderata from the matching literature: Pareto optimality and rank-maximality. Instead of asking the agents to report their complete preferences, our goal is to learn a desirable matching from partial preferences, specifically a matching that is necessarily Pareto optimal (NPO) or necessarily rank-maximal (NRM) under any completion of the partial preferences. We focus on the top-$k$ model in which agents reveal a prefix of their preference rankings. We design efficient algorithms to check if a given matching is NPO or NRM, and to check whether such a matching exists given top-$k$ partial preferences. We also study online algorithms to elicit partial preferences adaptively, and prove bounds on their competitive ratio.