Rohit Vaish
Graphical House Allocation
Jan 03, 2023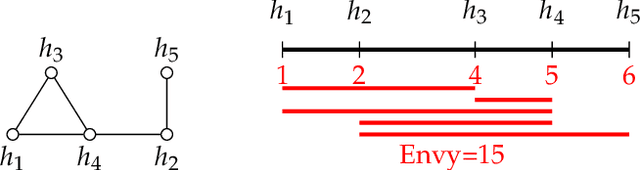


Abstract:The classical house allocation problem involves assigning $n$ houses (or items) to $n$ agents according to their preferences. A key criterion in such problems is satisfying some fairness constraints such as envy-freeness. We consider a generalization of this problem wherein the agents are placed along the vertices of a graph (corresponding to a social network), and each agent can only experience envy towards its neighbors. Our goal is to minimize the aggregate envy among the agents as a natural fairness objective, i.e., the sum of all pairwise envy values over all edges in a social graph. When agents have identical and evenly-spaced valuations, our problem reduces to the well-studied problem of linear arrangements. For identical valuations with possibly uneven spacing, we show a number of deep and surprising ways in which our setting is a departure from this classical problem. More broadly, we contribute several structural and computational results for various classes of graphs, including NP-hardness results for disjoint unions of paths, cycles, stars, or cliques, and fixed-parameter tractable (and, in some cases, polynomial-time) algorithms for paths, cycles, stars, cliques, and their disjoint unions. Additionally, a conceptual contribution of our work is the formulation of a structural property for disconnected graphs that we call separability which results in efficient parameterized algorithms for finding optimal allocations.
Minimizing Time-to-Rank: A Learning and Recommendation Approach
May 27, 2019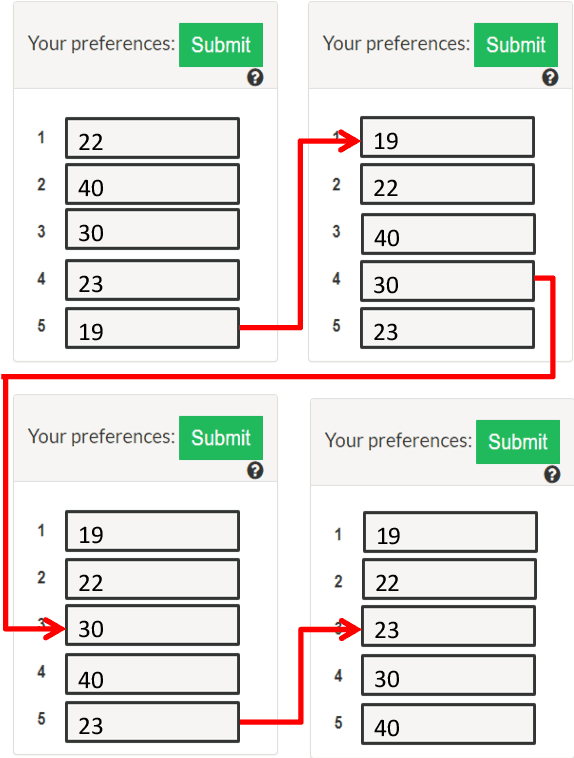
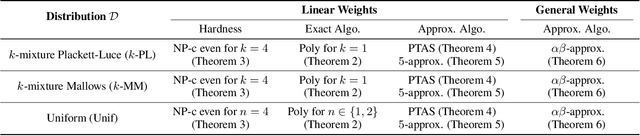


Abstract:Consider the following problem faced by an online voting platform: A user is provided with a list of alternatives, and is asked to rank them in order of preference using only drag-and-drop operations. The platform's goal is to recommend an initial ranking that minimizes the time spent by the user in arriving at her desired ranking. We develop the first optimization framework to address this problem, and make theoretical as well as practical contributions. On the practical side, our experiments on Amazon Mechanical Turk provide two interesting insights about user behavior: First, that users' ranking strategies closely resemble selection or insertion sort, and second, that the time taken for a drag-and-drop operation depends linearly on the number of positions moved. These insights directly motivate our theoretical model of the optimization problem. We show that computing an optimal recommendation is NP-hard, and provide exact and approximation algorithms for a variety of special cases of the problem. Experimental evaluation on MTurk shows that, compared to a random recommendation strategy, the proposed approach reduces the (average) time-to-rank by up to 50%.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge