Multi-Agent Risks from Advanced AI

The rapid development of advanced AI agents and the imminent deployment of many instances of these agents will give rise to multi-agent systems of unprecedented complexity. These systems pose novel and under-explored risks. In this report, we provide a structured taxonomy of these risks by identifying three key failure modes (miscoordination, conflict, and collusion) based on agents' incentives, as well as seven key risk factors (information asymmetries, network effects, selection pressures, destabilising dynamics, commitment problems, emergent agency, and multi-agent security) that can underpin them. We highlight several important instances of each risk, as well as promising directions to help mitigate them. By anchoring our analysis in a range of real-world examples and experimental evidence, we illustrate the distinct challenges posed by multi-agent systems and their implications for the safety, governance, and ethics of advanced AI.

Evolutionary Reinforcement Learning Dynamics with Irreducible Environmental Uncertainty

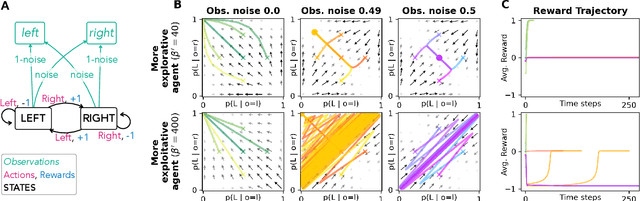
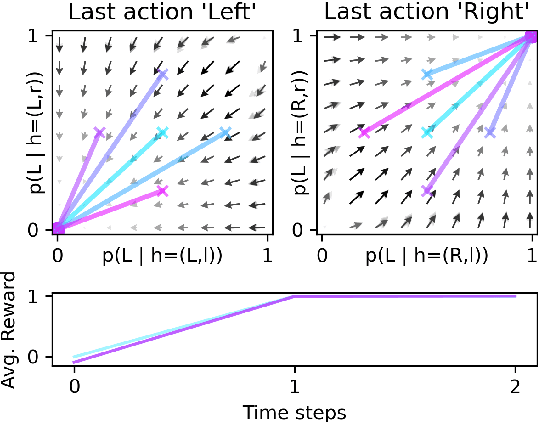
In this work we derive and present evolutionary reinforcement learning dynamics in which the agents are irreducibly uncertain about the current state of the environment. We evaluate the dynamics across different classes of partially observable agent-environment systems and find that irreducible environmental uncertainty can lead to better learning outcomes faster, stabilize the learning process and overcome social dilemmas. However, as expected, we do also find that partial observability may cause worse learning outcomes, for example, in the form of a catastrophic limit cycle. Compared to fully observant agents, learning with irreducible environmental uncertainty often requires more exploration and less weight on future rewards to obtain the best learning outcomes. Furthermore, we find a range of dynamical effects induced by partial observability, e.g., a critical slowing down of the learning processes between reward regimes and the separation of the learning dynamics into fast and slow directions. The presented dynamics are a practical tool for researchers in biology, social science and machine learning to systematically investigate the evolutionary effects of environmental uncertainty.

Deep reinforcement learning in World-Earth system models to discover sustainable management strategies

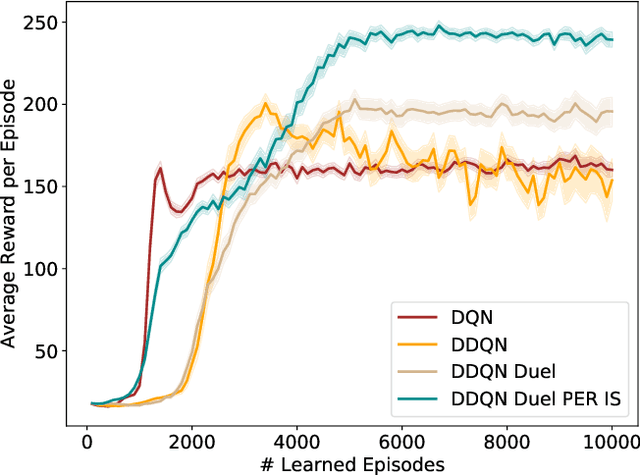
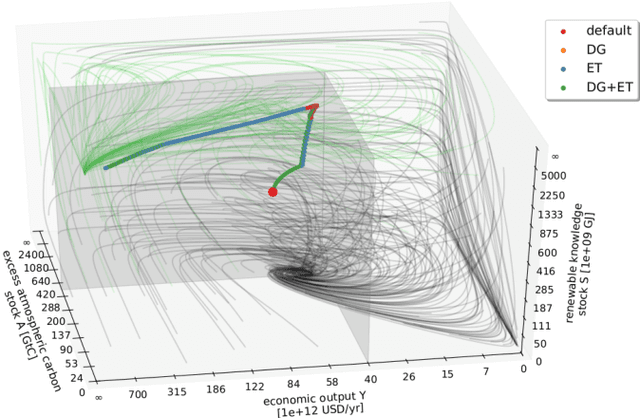
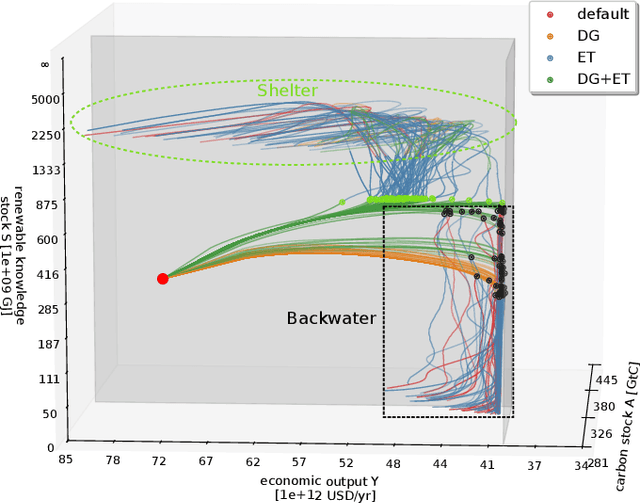
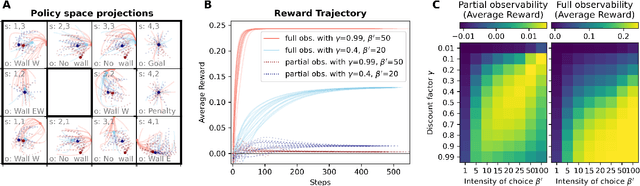
Increasingly complex, non-linear World-Earth system models are used for describing the dynamics of the biophysical Earth system and the socio-economic and socio-cultural World of human societies and their interactions. Identifying pathways towards a sustainable future in these models for informing policy makers and the wider public, e.g. pathways leading to a robust mitigation of dangerous anthropogenic climate change, is a challenging and widely investigated task in the field of climate research and broader Earth system science. This problem is particularly difficult when constraints on avoiding transgressions of planetary boundaries and social foundations need to be taken into account. In this work, we propose to combine recently developed machine learning techniques, namely deep reinforcement learning (DRL), with classical analysis of trajectories in the World-Earth system. Based on the concept of the agent-environment interface, we develop an agent that is generally able to act and learn in variable manageable environment models of the Earth system. We demonstrate the potential of our framework by applying DRL algorithms to two stylized World-Earth system models. Conceptually, we explore thereby the feasibility of finding novel global governance policies leading into a safe and just operating space constrained by certain planetary and socio-economic boundaries. The artificially intelligent agent learns that the timing of a specific mix of taxing carbon emissions and subsidies on renewables is of crucial relevance for finding World-Earth system trajectories that are sustainable on the long term.

Parsimonious modeling with Information Filtering Networks

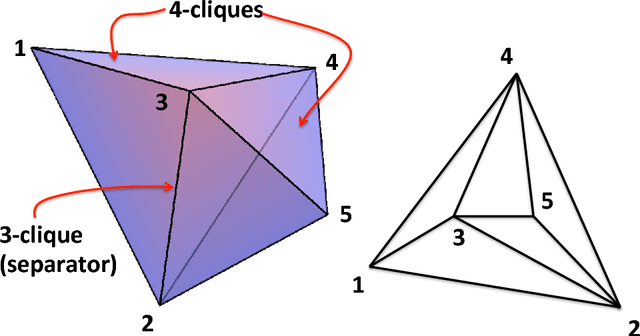
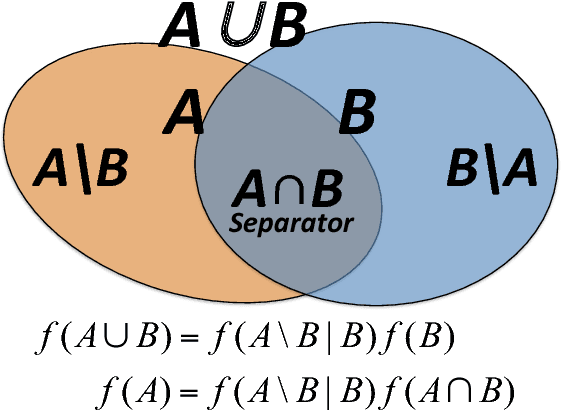
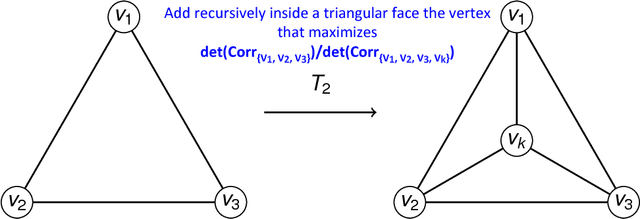
We introduce a methodology to construct parsimonious probabilistic models. This method makes use of Information Filtering Networks to produce a robust estimate of the global sparse inverse covariance from a simple sum of local inverse covariances computed on small sub-parts of the network. Being based on local and low-dimensional inversions, this method is computationally very efficient and statistically robust even for the estimation of inverse covariance of high-dimensional, noisy and short time-series. Applied to financial data our method results computationally more efficient than state-of-the-art methodologies such as Glasso producing, in a fraction of the computation time, models that can have equivalent or better performances but with a sparser inference structure. We also discuss performances with sparse factor models where we notice that relative performances decrease with the number of factors. The local nature of this approach allows us to perform computations in parallel and provides a tool for dynamical adaptation by partial updating when the properties of some variables change without the need of recomputing the whole model. This makes this approach particularly suitable to handle big datasets with large numbers of variables. Examples of practical application for forecasting, stress testing and risk allocation in financial systems are also provided.