A Novel approach to portfolio construction

This paper proposes a machine learning-based framework for asset selection and portfolio construction, termed the Best-Path Algorithm Sparse Graphical Model (BPASGM). The method extends the Best-Path Algorithm (BPA) by mapping linear and non-linear dependencies among a large set of financial assets into a sparse graphical model satisfying a structural Markov property. Based on this representation, BPASGM performs a dependence-driven screening that removes positively or redundantly connected assets, isolating subsets that are conditionally independent or negatively correlated. This step is designed to enhance diversification and reduce estimation error in high-dimensional portfolio settings. Portfolio optimization is then conducted on the selected subset using standard mean-variance techniques. BPASGM does not aim to improve the theoretical mean-variance optimum under known population parameters, but rather to enhance realized performance in finite samples, where sample-based Markowitz portfolios are highly sensitive to estimation error. Monte Carlo simulations show that BPASGM-based portfolios achieve more stable risk-return profiles, lower realized volatility, and superior risk-adjusted performance compared to standard mean-variance portfolios. Empirical results for U.S. equities, global stock indices, and foreign exchange rates over 1990-2025 confirm these findings and demonstrate a substantial reduction in portfolio cardinality. Overall, BPASGM offers a statistically grounded and computationally efficient framework that integrates sparse graphical modeling with portfolio theory for dependence-aware asset selection.

A new multilayer network construction via Tensor learning

Multilayer networks proved to be suitable in extracting and providing dependency information of different complex systems. The construction of these networks is difficult and is mostly done with a static approach, neglecting time delayed interdependences. Tensors are objects that naturally represent multilayer networks and in this paper, we propose a new methodology based on Tucker tensor autoregression in order to build a multilayer network directly from data. This methodology captures within and between connections across layers and makes use of a filtering procedure to extract relevant information and improve visualization. We show the application of this methodology to different stationary fractionally differenced financial data. We argue that our result is useful to understand the dependencies across three different aspects of financial risk, namely market risk, liquidity risk, and volatility risk. Indeed, we show how the resulting visualization is a useful tool for risk managers depicting dependency asymmetries between different risk factors and accounting for delayed cross dependencies. The constructed multilayer network shows a strong interconnection between the volumes and prices layers across all the stocks considered while a lower number of interconnections between the uncertainty measures is identified.

Predicting Multidimensional Data via Tensor Learning

The analysis of multidimensional data is becoming a more and more relevant topic in statistical and machine learning research. Given their complexity, such data objects are usually reshaped into matrices or vectors and then analysed. However, this methodology presents several drawbacks. First of all, it destroys the intrinsic interconnections among datapoints in the multidimensional space and, secondly, the number of parameters to be estimated in a model increases exponentially. We develop a model that overcomes such drawbacks. In particular, we proposed a parsimonious tensor regression based model that retains the intrinsic multidimensional structure of the dataset. Tucker structure is employed to achieve parsimony and a shrinkage penalization is introduced to deal with over-fitting and collinearity. An Alternating Least Squares (ALS) algorithm is developed to estimate the model parameters. A simulation exercise is produced to validate the model and its robustness. Finally, an empirical application to Foursquares spatio-temporal dataset and macroeconomic time series is also performed. Overall, the proposed model is able to outperform existing models present in forecasting literature.

Parsimonious modeling with Information Filtering Networks

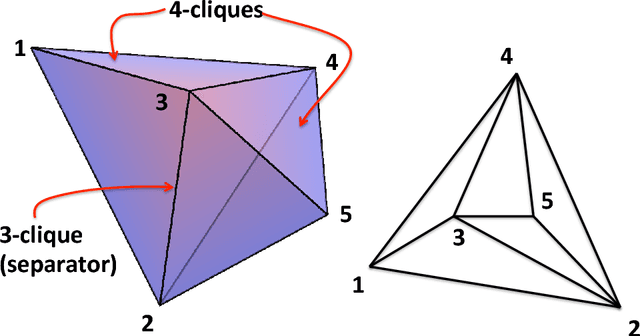
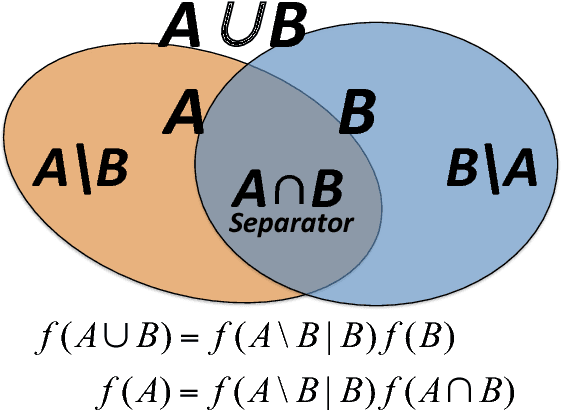
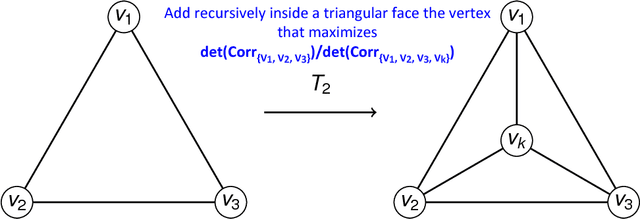
We introduce a methodology to construct parsimonious probabilistic models. This method makes use of Information Filtering Networks to produce a robust estimate of the global sparse inverse covariance from a simple sum of local inverse covariances computed on small sub-parts of the network. Being based on local and low-dimensional inversions, this method is computationally very efficient and statistically robust even for the estimation of inverse covariance of high-dimensional, noisy and short time-series. Applied to financial data our method results computationally more efficient than state-of-the-art methodologies such as Glasso producing, in a fraction of the computation time, models that can have equivalent or better performances but with a sparser inference structure. We also discuss performances with sparse factor models where we notice that relative performances decrease with the number of factors. The local nature of this approach allows us to perform computations in parallel and provides a tool for dynamical adaptation by partial updating when the properties of some variables change without the need of recomputing the whole model. This makes this approach particularly suitable to handle big datasets with large numbers of variables. Examples of practical application for forecasting, stress testing and risk allocation in financial systems are also provided.