Learning-Augmented Robust Algorithmic Recourse

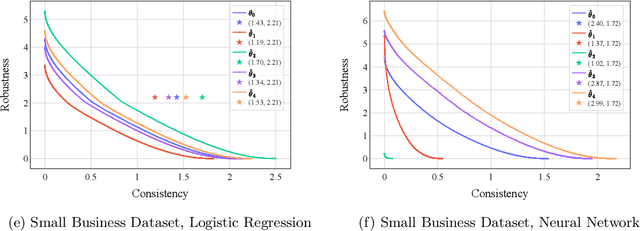
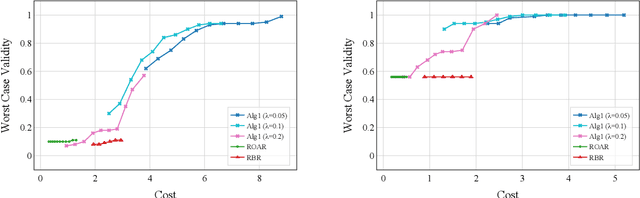
The widespread use of machine learning models in high-stakes domains can have a major negative impact, especially on individuals who receive undesirable outcomes. Algorithmic recourse provides such individuals with suggestions of minimum-cost improvements they can make to achieve a desirable outcome in the future. However, machine learning models often get updated over time and this can cause a recourse to become invalid (i.e., not lead to the desirable outcome). The robust recourse literature aims to choose recourses that are less sensitive, even against adversarial model changes, but this comes at a higher cost. To overcome this obstacle, we initiate the study of algorithmic recourse through the learning-augmented framework and evaluate the extent to which a designer equipped with a prediction regarding future model changes can reduce the cost of recourse when the prediction is accurate (consistency) while also limiting the cost even when the prediction is inaccurate (robustness). We propose a novel algorithm for this problem, study the robustness-consistency trade-off, and analyze how prediction accuracy affects performance.

Best of Both Distortion Worlds

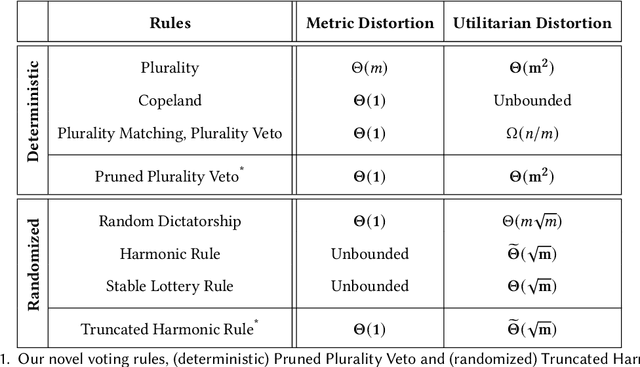
We study the problem of designing voting rules that take as input the ordinal preferences of $n$ agents over a set of $m$ alternatives and output a single alternative, aiming to optimize the overall happiness of the agents. The input to the voting rule is each agent's ranking of the alternatives from most to least preferred, yet the agents have more refined (cardinal) preferences that capture the intensity with which they prefer one alternative over another. To quantify the extent to which voting rules can optimize over the cardinal preferences given access only to the ordinal ones, prior work has used the distortion measure, i.e., the worst-case approximation ratio between a voting rule's performance and the best performance achievable given the cardinal preferences. The work on the distortion of voting rules has been largely divided into two worlds: utilitarian distortion and metric distortion. In the former, the cardinal preferences of the agents correspond to general utilities and the goal is to maximize a normalized social welfare. In the latter, the agents' cardinal preferences correspond to costs given by distances in an underlying metric space and the goal is to minimize the (unnormalized) social cost. Several deterministic and randomized voting rules have been proposed and evaluated for each of these worlds separately, gradually improving the achievable distortion bounds, but none of the known voting rules perform well in both worlds simultaneously. In this work, we prove that one can achieve the best of both worlds by designing new voting rules, that simultaneously achieve near-optimal distortion guarantees in both distortion worlds. We also prove that this positive result does not generalize to the case where the voting rule is provided with the rankings of only the top-$t$ alternatives of each agent, for $t<m$.

PROPm Allocations of Indivisible Goods to Multiple Agents

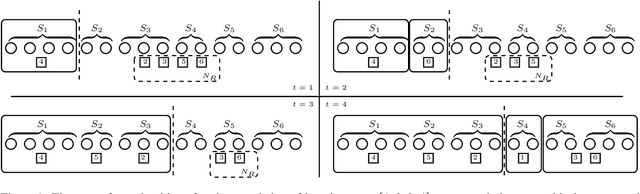
We study the classic problem of fairly allocating a set of indivisible goods among a group of agents, and focus on the notion of approximate proportionality known as PROPm. Prior work showed that there exists an allocation that satisfies this notion of fairness for instances involving up to five agents, but fell short of proving that this is true in general. We extend this result to show that a PROPm allocation is guaranteed to exist for all instances, independent of the number of agents or goods. Our proof is constructive, providing an algorithm that computes such an allocation and, unlike prior work, the running time of this algorithm is polynomial in both the number of agents and the number of goods.

Achieving Proportionality up to the Maximin Item with Indivisible Goods

We study the problem of fairly allocating indivisible goods and focus on the classic fairness notion of proportionality. The indivisibility of the goods is long known to pose highly non-trivial obstacles to achieving fairness, and a very vibrant line of research has aimed to circumvent them using appropriate notions of approximate fairness. Recent work has established that even approximate versions of proportionality (PROPx) may be impossible to achieve even for small instances, while the best known achievable approximations (PROP1) are much weaker. We introduce the notion of proportionality up to the maximin item (PROPm) and show how to reach an allocation satisfying this notion for any instance involving up to five agents with additive valuations. PROPm provides a well motivated middle-ground between PROP1 and PROPx, while also capturing some elements of the well-studied maximin share (MMS) benchmark: another relaxation of proportionality that has attracted a lot of attention.

Resolving the Optimal Metric Distortion Conjecture

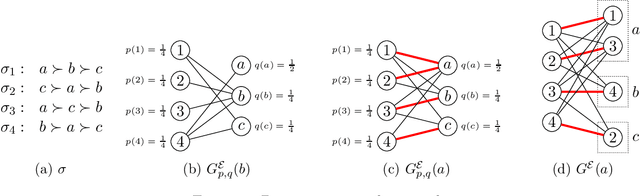
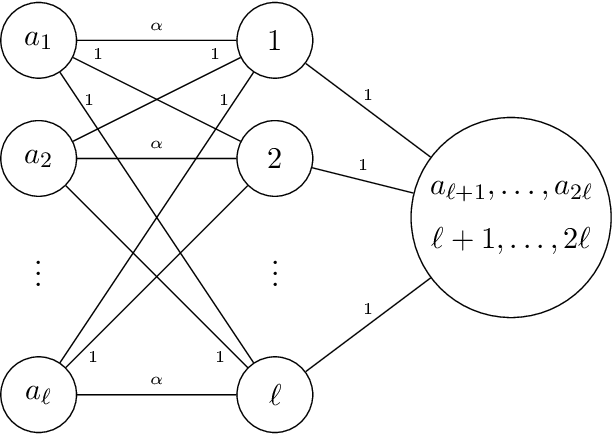
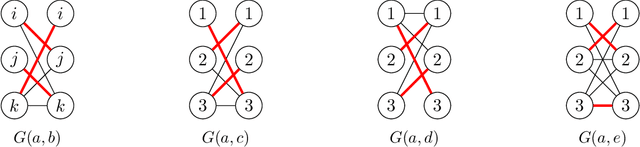
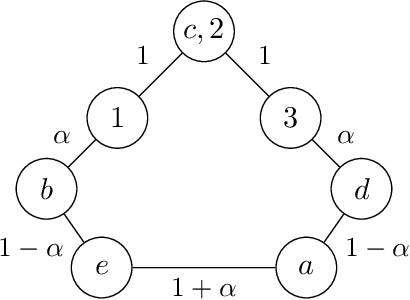
We study the following metric distortion problem: there are two finite sets of points, V and C, that lie in the same metric space, and our goal is to choose a point in C whose total distance from the points in V is as small as possible. However, rather than having access to the underlying distance metric, we only know, for each point in V , a ranking of its distances to the points in C. We propose algorithms that choose a point in C using only these rankings as input and we provide bounds on their distortion (worst-case approximation ratio). A prominent motivation for this problem comes from voting theory, where V represents a set of voters, C represents a set of candidates, and the rankings correspond to ordinal preferences of the voters. A major conjecture in this framework is that the optimal deterministic algorithm has distortion 3. We resolve this conjecture by providing a polynomial-time algorithm that achieves distortion 3, matching a known lower bound. We do so by proving a novel lemma about matching rankings of candidates to candidates, which we refer to as the ranking-matching lemma. This lemma induces a family of novel algorithms, which may be of independent interest, and we show that a special algorithm in this family achieves distortion 3. We also provide more refined, parameterized, bounds using the notion of {\alpha}-decisiveness, which quantifies the extent to which a voter may prefer her top choice relative to all others. Finally, we introduce a new randomized algorithm with improved distortion compared to known results, and also provide improved lower bounds on the distortion of all deterministic and randomized algorithms.

Balanced Ranking with Diversity Constraints

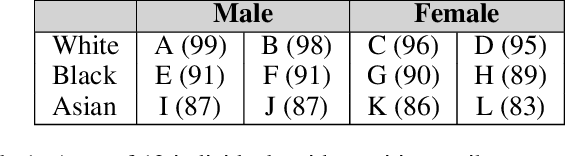
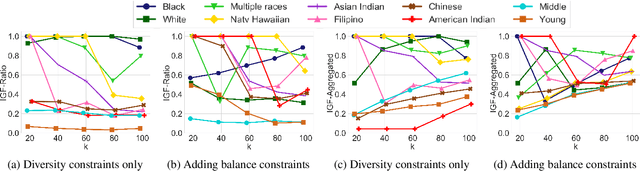
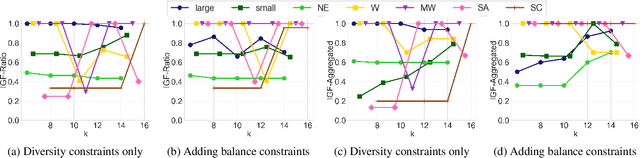
Many set selection and ranking algorithms have recently been enhanced with diversity constraints that aim to explicitly increase representation of historically disadvantaged populations, or to improve the overall representativeness of the selected set. An unintended consequence of these constraints, however, is reduced in-group fairness: the selected candidates from a given group may not be the best ones, and this unfairness may not be well-balanced across groups. In this paper we study this phenomenon using datasets that comprise multiple sensitive attributes. We then introduce additional constraints, aimed at balancing the \in-group fairness across groups, and formalize the induced optimization problems as integer linear programs. Using these programs, we conduct an experimental evaluation with real datasets, and quantify the feasible trade-offs between balance and overall performance in the presence of diversity constraints.