Axioms for AI Alignment from Human Feedback

In the context of reinforcement learning from human feedback (RLHF), the reward function is generally derived from maximum likelihood estimation of a random utility model based on pairwise comparisons made by humans. The problem of learning a reward function is one of preference aggregation that, we argue, largely falls within the scope of social choice theory. From this perspective, we can evaluate different aggregation methods via established axioms, examining whether these methods meet or fail well-known standards. We demonstrate that both the Bradley-Terry-Luce Model and its broad generalizations fail to meet basic axioms. In response, we develop novel rules for learning reward functions with strong axiomatic guarantees. A key innovation from the standpoint of social choice is that our problem has a linear structure, which greatly restricts the space of feasible rules and leads to a new paradigm that we call linear social choice.

Computing Voting Rules with Elicited Incomplete Votes

Motivated by the difficulty of specifying complete ordinal preferences over a large set of $m$ candidates, we study voting rules that are computable by querying voters about $t < m$ candidates. Generalizing prior works that focused on specific instances of this problem, our paper fully characterizes the set of positional scoring rules that can be computed for any $1 \leq t < m$, which notably does not include plurality. We then extend this to show a similar impossibility result for single transferable vote (elimination voting). These negative results are information-theoretic and agnostic to the number of queries. Finally, for scoring rules that are computable with limited-sized queries, we give parameterized upper and lower bounds on the number of such queries a deterministic or randomized algorithm must make to determine the score-maximizing candidate. While there is no gap between our bounds for deterministic algorithms, identifying the exact query complexity for randomized algorithms is a challenging open problem, of which we solve one special case.

The Optimal Size of an Epistemic Congress

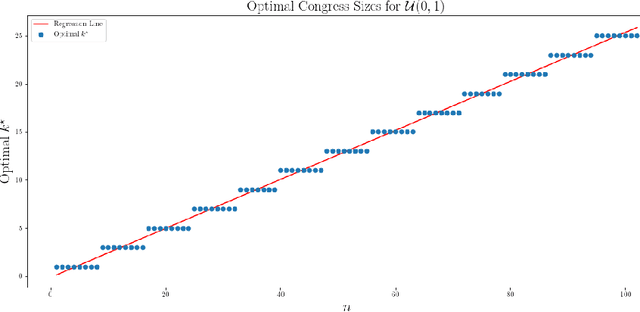
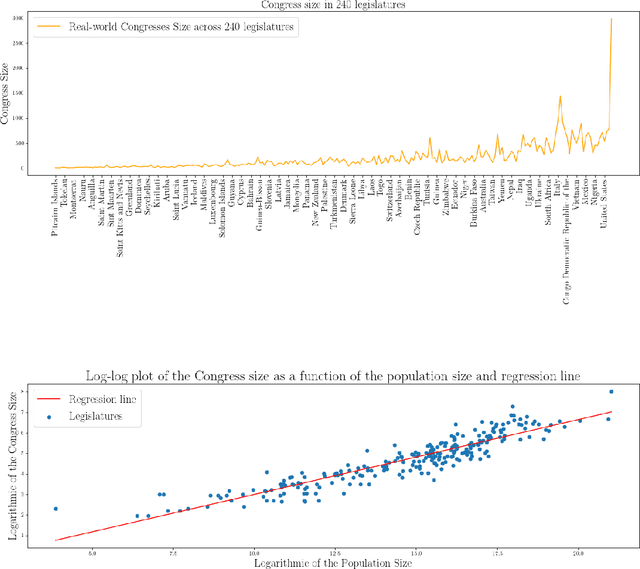
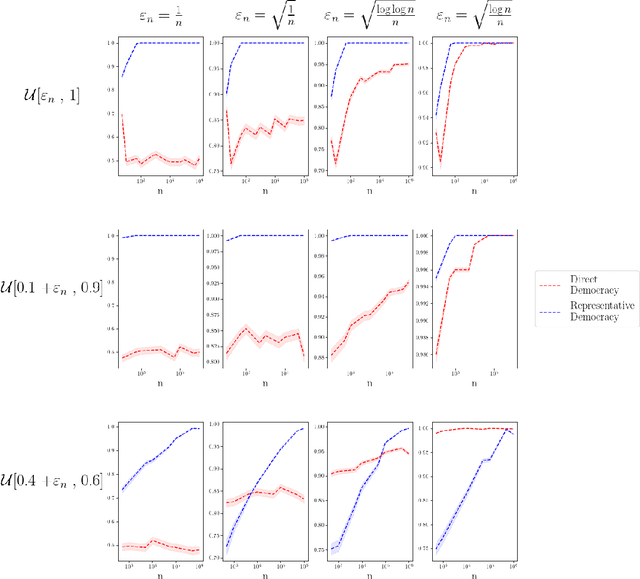
We analyze the optimal size of a congress in a representative democracy. We take an epistemic view where voters decide on a binary issue with one ground truth outcome, and each voter votes correctly according to their competence levels in $[0, 1]$. Assuming that we can sample the best experts to form an epistemic congress, we find that the optimal congress size should be linear in the population size. This result is striking because it holds even when allowing the top representatives to be accurate with arbitrarily high probabilities. We then analyze real world data, finding that the actual sizes of congresses are much smaller than the optimal size our theoretical results suggest. We conclude by analyzing under what conditions congresses of sub-optimal sizes would still outperform direct democracy, in which all voters vote.

Fair and Efficient Resource Allocation with Partial Information

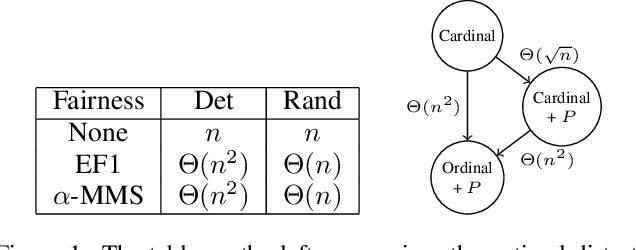
We study the fundamental problem of allocating indivisible goods to agents with additive preferences. We consider eliciting from each agent only a ranking of her $k$ most preferred goods instead of her full cardinal valuations. We characterize the value of $k$ needed to achieve envy-freeness up to one good and approximate maximin share guarantee, two widely studied fairness notions. We also analyze the multiplicative loss in social welfare incurred due to the lack of full information with and without the fairness requirements.

Resolving the Optimal Metric Distortion Conjecture

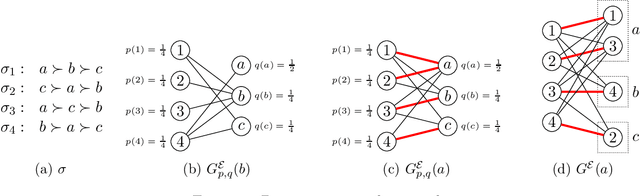
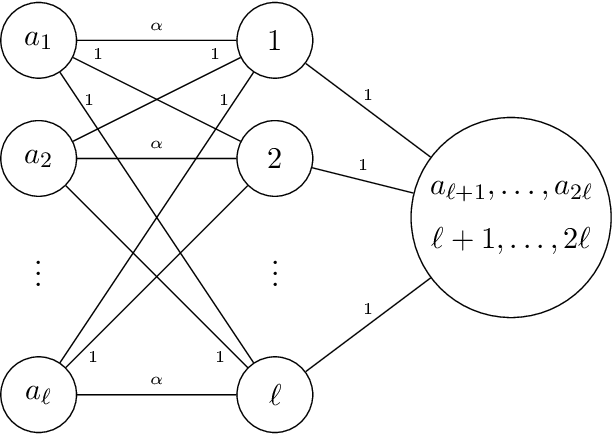
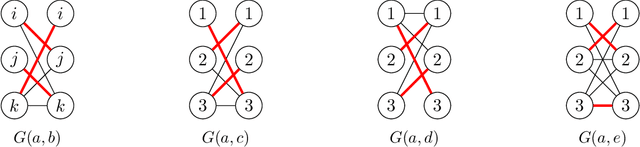
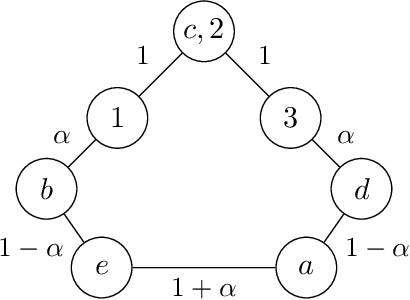
We study the following metric distortion problem: there are two finite sets of points, V and C, that lie in the same metric space, and our goal is to choose a point in C whose total distance from the points in V is as small as possible. However, rather than having access to the underlying distance metric, we only know, for each point in V , a ranking of its distances to the points in C. We propose algorithms that choose a point in C using only these rankings as input and we provide bounds on their distortion (worst-case approximation ratio). A prominent motivation for this problem comes from voting theory, where V represents a set of voters, C represents a set of candidates, and the rankings correspond to ordinal preferences of the voters. A major conjecture in this framework is that the optimal deterministic algorithm has distortion 3. We resolve this conjecture by providing a polynomial-time algorithm that achieves distortion 3, matching a known lower bound. We do so by proving a novel lemma about matching rankings of candidates to candidates, which we refer to as the ranking-matching lemma. This lemma induces a family of novel algorithms, which may be of independent interest, and we show that a special algorithm in this family achieves distortion 3. We also provide more refined, parameterized, bounds using the notion of {\alpha}-decisiveness, which quantifies the extent to which a voter may prefer her top choice relative to all others. Finally, we introduce a new randomized algorithm with improved distortion compared to known results, and also provide improved lower bounds on the distortion of all deterministic and randomized algorithms.