Jonathan Johannemann
Sufficient Representations for Categorical Variables
Aug 26, 2019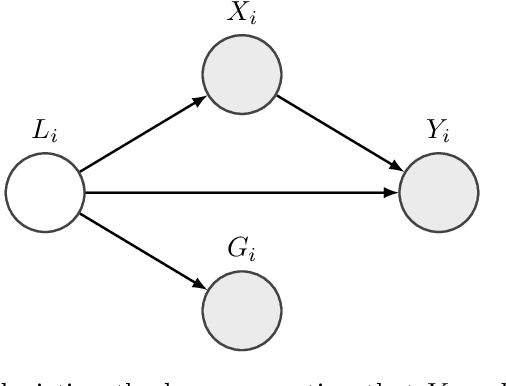
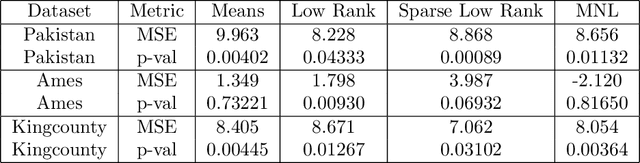
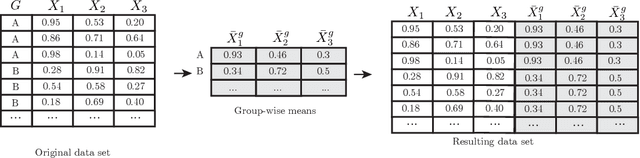
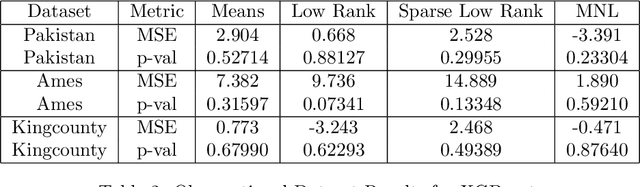
Abstract:Many learning algorithms require categorical data to be transformed into real vectors before it can be used as input. Often, categorical variables are encoded as one-hot (or dummy) vectors. However, this mode of representation can be wasteful since it adds many low-signal regressors, especially when the number of unique categories is large. In this paper, we investigate simple alternative solutions for universally consistent estimators that rely on lower-dimensional real-valued representations of categorical variables that are "sufficient" in the sense that no predictive information is lost. We then compare preexisting and proposed methods on simulated and observational datasets.
Spectral Overlap and a Comparison of Parameter-Free, Dimensionality Reduction Quality Metrics
Jul 03, 2019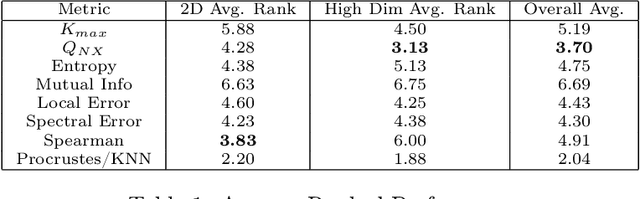

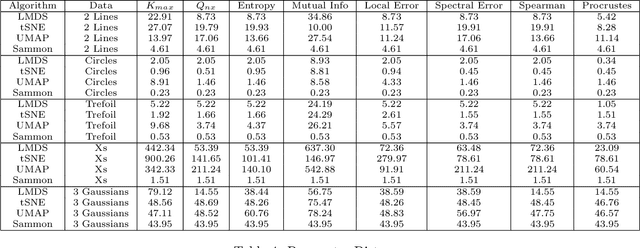
Abstract:Nonlinear dimensionality reduction methods are a popular tool for data scientists and researchers to visualize complex, high dimensional data. However, while these methods continue to improve and grow in number, it is often difficult to evaluate the quality of a visualization due to a variety of factors such as lack of information about the intrinsic dimension of the data and additional tuning required for many evaluation metrics. In this paper, we seek to provide a systematic comparison of dimensionality reduction quality metrics using datasets where we know the ground truth manifold. We utilize each metric for hyperparameter optimization in popular dimensionality reduction methods used for visualization and provide quantitative metrics to objectively compare visualizations to their original manifold. In our results, we find a few methods that appear to consistently do well and propose the best performer as a benchmark for evaluating dimensionality reduction based visualizations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge