Optimal Balancing of Time-Dependent Confounders for Marginal Structural Models
Paper and Code
Jun 04, 2018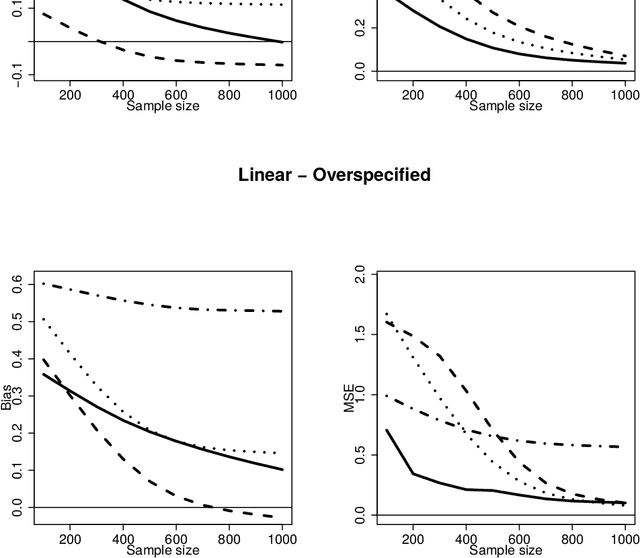

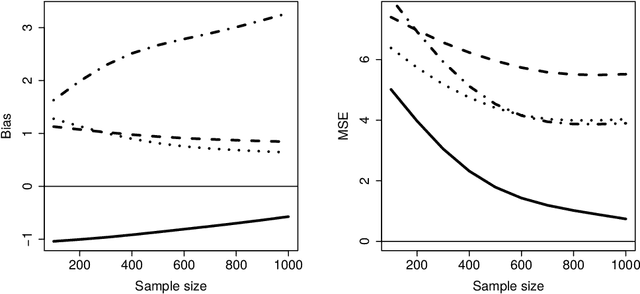
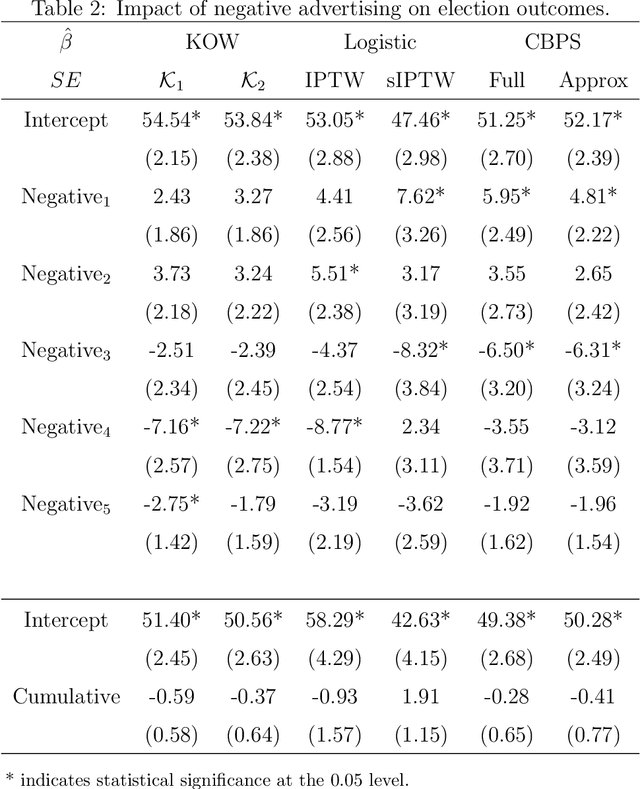
Marginal structural models (MSMs) estimate the causal effect of a time-varying treatment in the presence of time-dependent confounding via weighted regression. The standard approach of using inverse probability of treatment weighting (IPTW) can lead to high-variance estimates due to extreme weights and be sensitive to model misspecification. Various methods have been proposed to partially address this, including truncation and stabilized-IPTW to temper extreme weights and covariate balancing propensity score (CBPS) to address treatment model misspecification. In this paper, we present Kernel Optimal Weighting (KOW), a convex-optimization-based approach that finds weights for fitting the MSM that optimally balance time-dependent confounders while simultaneously controlling for precision, directly addressing the above limitations. KOW directly minimizes the error in estimation due to time-dependent confounding via a new decomposition as a functional. We further extend KOW to control for informative censoring. We evaluate the performance of KOW in a simulation study, comparing it with IPTW, stabilized-IPTW, and CBPS. We demonstrate the use of KOW in studying the effect of treatment initiation on time-to-death among people living with HIV and the effect of negative advertising on elections in the United States.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge