On Robust Optimal Transport: Computational Complexity, Low-rank Approximation, and Barycenter Computation
Paper and Code
Feb 13, 2021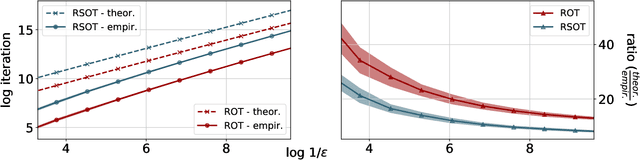

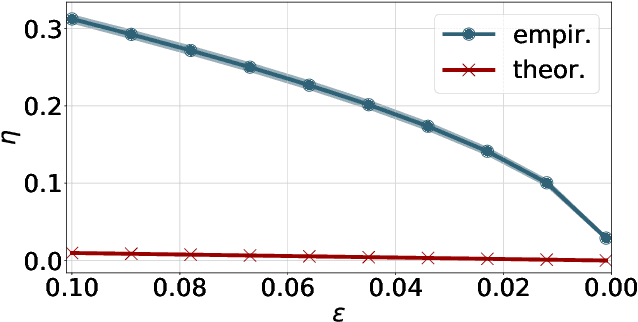
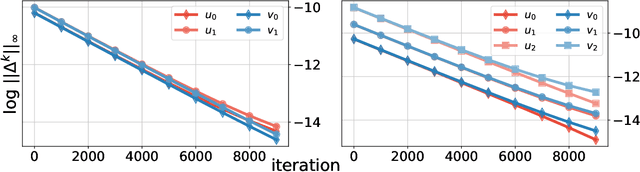
We consider two robust versions of optimal transport, named $\textit{Robust Semi-constrained Optimal Transport}$ (RSOT) and $\textit{Robust Unconstrained Optimal Transport}$ (ROT), formulated by relaxing the marginal constraints with Kullback-Leibler divergence. For both problems in the discrete settings, we propose Sinkhorn-based algorithms that produce $\varepsilon$-approximations of RSOT and ROT in $\widetilde{\mathcal{O}}(\frac{n^2}{\varepsilon})$ time, where $n$ is the number of supports of the probability distributions. Furthermore, to reduce the dependency of the complexity of the Sinkhorn-based algorithms on $n$, we apply Nystr\"{o}m method to approximate the kernel matrix in both RSOT and ROT by a matrix of rank $r$ before passing it to these Sinkhorn-based algorithms. We demonstrate that these new algorithms have $\widetilde{\mathcal{O}}(n r^2 + \frac{nr}{\varepsilon})$ runtime to obtain the RSOT and ROT $\varepsilon$-approximations. Finally, we consider a barycenter problem based on RSOT, named $\textit{Robust Semi-Constrained Barycenter}$ problem (RSBP), and develop a robust iterative Bregman projection algorithm, called $\textbf{Normalized-RobustIBP}$ algorithm, to solve the RSBP in the discrete settings of probability distributions. We show that an $\varepsilon$-approximated solution of the RSBP can be achieved in $\widetilde{\mathcal{O}}(\frac{mn^2}{\varepsilon})$ time using $\textbf{Normalized-RobustIBP}$ algorithm when $m = 2$, which is better than the previous complexity $\widetilde{\mathcal{O}}(\frac{mn^2}{\varepsilon^2})$ of IBP algorithm for approximating the Wasserstein barycenter. Extensive experiments confirm our theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge