Dendrogram of mixing measures: Hierarchical clustering and model selection for finite mixture models

We present a new way to summarize and select mixture models via the hierarchical clustering tree (dendrogram) constructed from an overfitted latent mixing measure. Our proposed method bridges agglomerative hierarchical clustering and mixture modeling. The dendrogram's construction is derived from the theory of convergence of the mixing measures, and as a result, we can both consistently select the true number of mixing components and obtain the pointwise optimal convergence rate for parameter estimation from the tree, even when the model parameters are only weakly identifiable. In theory, it explicates the choice of the optimal number of clusters in hierarchical clustering. In practice, the dendrogram reveals more information on the hierarchy of subpopulations compared to traditional ways of summarizing mixture models. Several simulation studies are carried out to support our theory. We also illustrate the methodology with an application to single-cell RNA sequence analysis.

Strong identifiability and parameter learning in regression with heterogeneous response

Mixtures of regression are a powerful class of models for regression learning with respect to a highly uncertain and heterogeneous response variable of interest. In addition to being a rich predictive model for the response given some covariates, the parameters in this model class provide useful information about the heterogeneity in the data population, which is represented by the conditional distributions for the response given the covariates associated with a number of distinct but latent subpopulations. In this paper, we investigate conditions of strong identifiability, rates of convergence for conditional density and parameter estimation, and the Bayesian posterior contraction behavior arising in finite mixture of regression models, under exact-fitted and over-fitted settings and when the number of components is unknown. This theory is applicable to common choices of link functions and families of conditional distributions employed by practitioners. We provide simulation studies and data illustrations, which shed some light on the parameter learning behavior found in several popular regression mixture models reported in the literature.

Beyond Black Box Densities: Parameter Learning for the Deviated Components

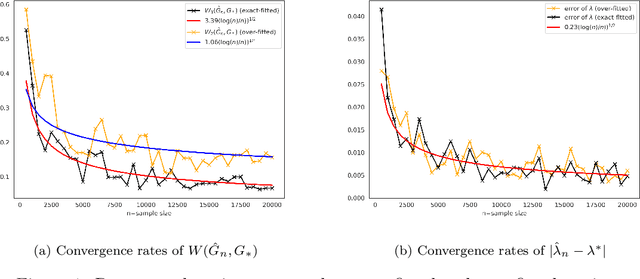
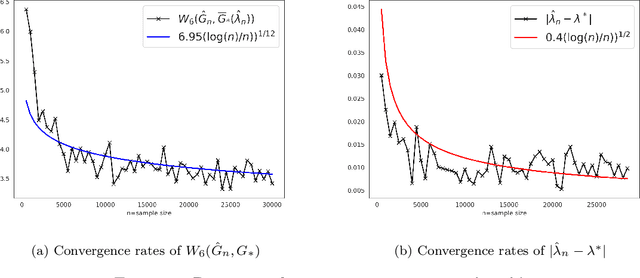
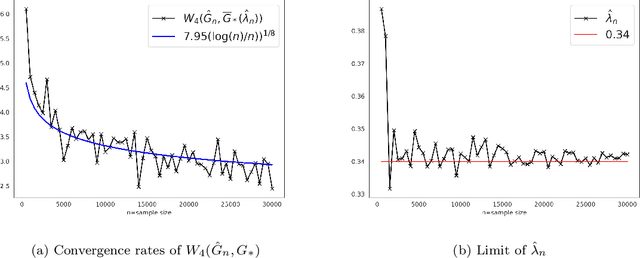
As we collect additional samples from a data population for which a known density function estimate may have been previously obtained by a black box method, the increased complexity of the data set may result in the true density being deviated from the known estimate by a mixture distribution. To model this phenomenon, we consider the \emph{deviating mixture model} $(1-\lambda^{*})h_0 + \lambda^{*} (\sum_{i = 1}^{k} p_{i}^{*} f(x|\theta_{i}^{*}))$, where $h_0$ is a known density function, while the deviated proportion $\lambda^{*}$ and latent mixing measure $G_{*} = \sum_{i = 1}^{k} p_{i}^{*} \delta_{\theta_i^{*}}$ associated with the mixture distribution are unknown. Via a novel notion of distinguishability between the known density $h_{0}$ and the deviated mixture distribution, we establish rates of convergence for the maximum likelihood estimates of $\lambda^{*}$ and $G^{*}$ under Wasserstein metric. Simulation studies are carried out to illustrate the theory.

On Label Shift in Domain Adaptation via Wasserstein Distance

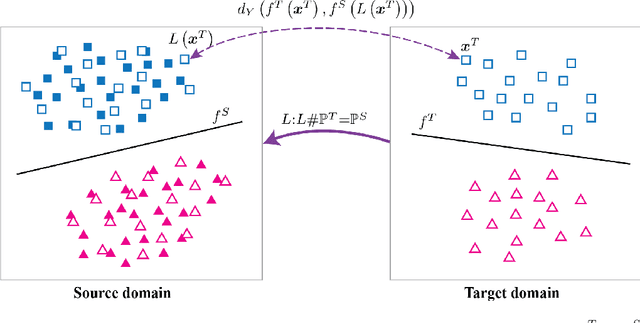
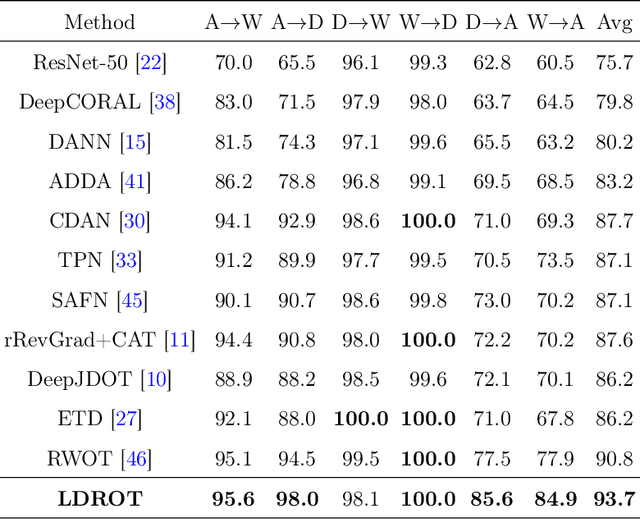
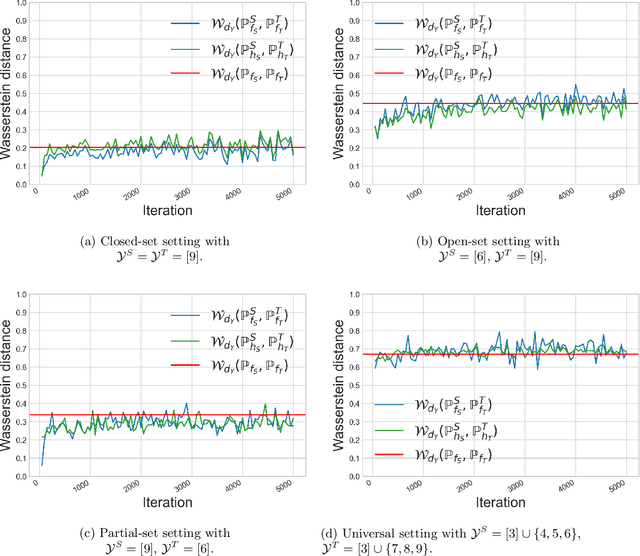
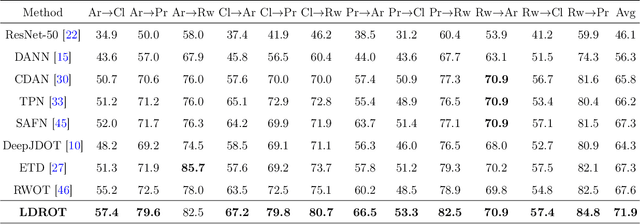
We study the label shift problem between the source and target domains in general domain adaptation (DA) settings. We consider transformations transporting the target to source domains, which enable us to align the source and target examples. Through those transformations, we define the label shift between two domains via optimal transport and develop theory to investigate the properties of DA under various DA settings (e.g., closed-set, partial-set, open-set, and universal settings). Inspired from the developed theory, we propose Label and Data Shift Reduction via Optimal Transport (LDROT) which can mitigate the data and label shifts simultaneously. Finally, we conduct comprehensive experiments to verify our theoretical findings and compare LDROT with state-of-the-art baselines.

Entropic Gromov-Wasserstein between Gaussian Distributions

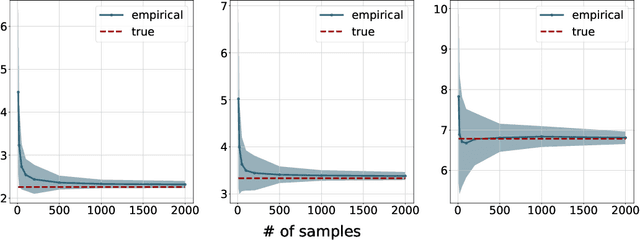
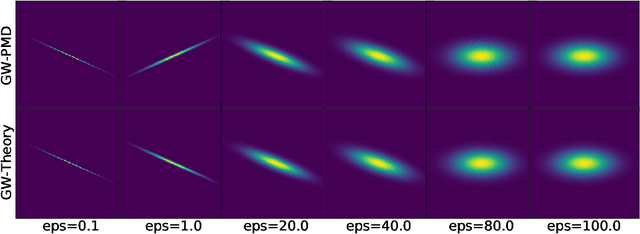
We study the entropic Gromov-Wasserstein and its unbalanced version between (unbalanced) Gaussian distributions with different dimensions. When the metric is the inner product, which we refer to as inner product Gromov-Wasserstein (IGW), we demonstrate that the optimal transportation plans of entropic IGW and its unbalanced variant are (unbalanced) Gaussian distributions. Via an application of von Neumann's trace inequality, we obtain closed-form expressions for the entropic IGW between these Gaussian distributions. Finally, we consider an entropic inner product Gromov-Wasserstein barycenter of multiple Gaussian distributions. We prove that the barycenter is Gaussian distribution when the entropic regularization parameter is small. We further derive closed-form expressions for the covariance matrix of the barycenter.