On Barycenter Computation: Semi-Unbalanced Optimal Transport-based Method on Gaussians
Paper and Code
Oct 10, 2024

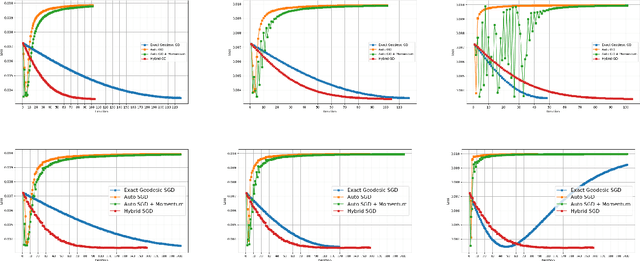
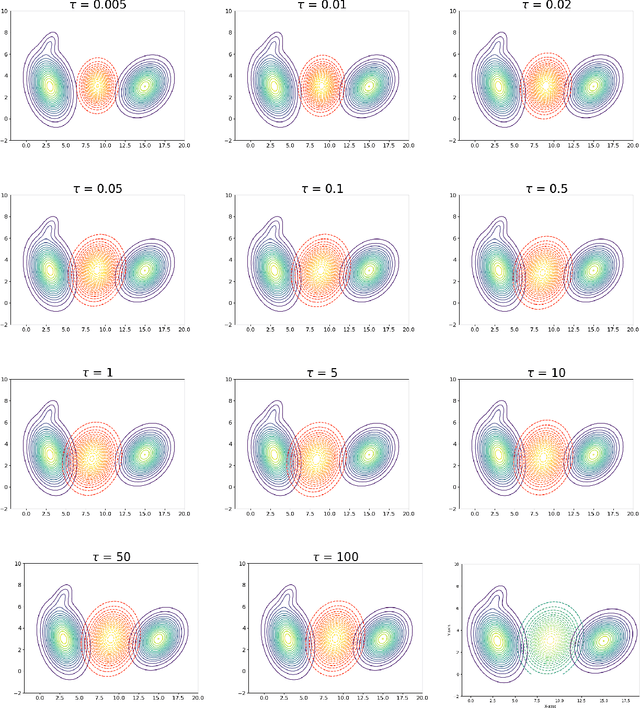
We explore a robust version of the barycenter problem among $n$ centered Gaussian probability measures, termed Semi-Unbalanced Optimal Transport (SUOT)-based Barycenter, wherein the barycenter remains fixed while the others are relaxed using Kullback-Leibler divergence. We develop optimization algorithms on Bures-Wasserstein manifold, named the Exact Geodesic Gradient Descent and Hybrid Gradient Descent algorithms. While the Exact Geodesic Gradient Descent method is based on computing the exact closed form of the first-order derivative of the objective function of the barycenter along a geodesic on the Bures manifold, the Hybrid Gradient Descent method utilizes optimizer components when solving the SUOT problem to replace outlier measures before applying the Riemannian Gradient Descent. We establish the theoretical convergence guarantees for both methods and demonstrate that the Exact Geodesic Gradient Descent algorithm attains a dimension-free convergence rate. Finally, we conduct experiments to compare the normal Wasserstein Barycenter with ours and perform an ablation study.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge