On Barycenter Computation: Semi-Unbalanced Optimal Transport-based Method on Gaussians

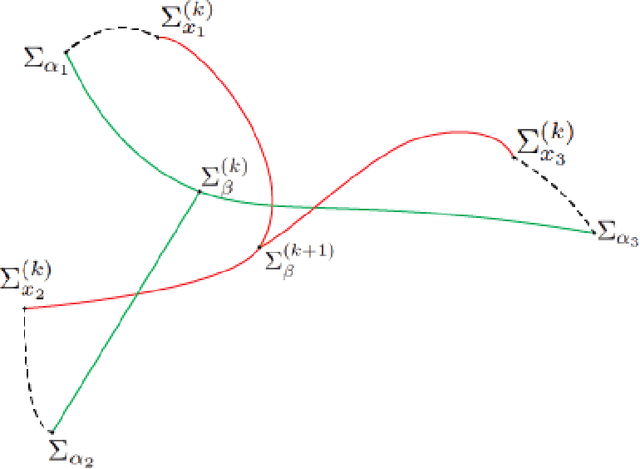
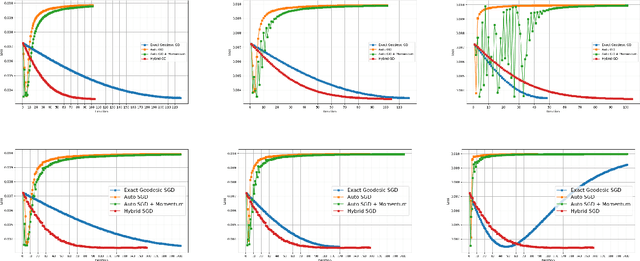
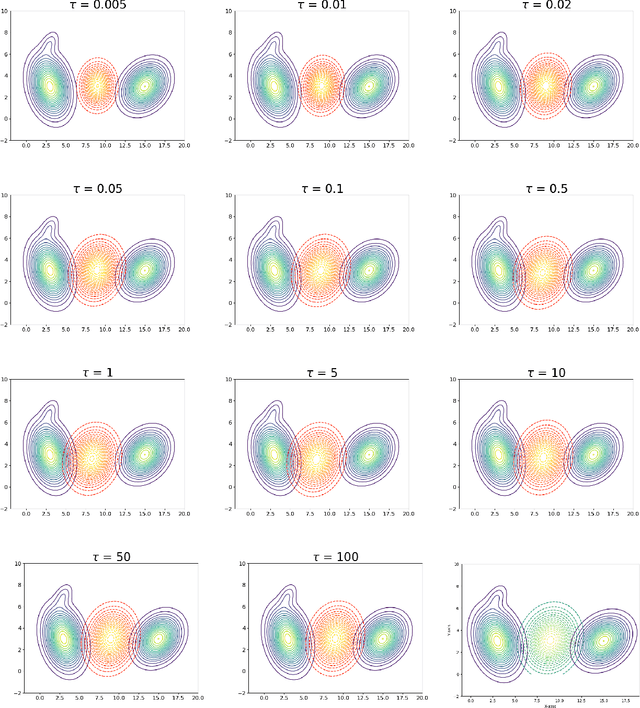
We explore a robust version of the barycenter problem among $n$ centered Gaussian probability measures, termed Semi-Unbalanced Optimal Transport (SUOT)-based Barycenter, wherein the barycenter remains fixed while the others are relaxed using Kullback-Leibler divergence. We develop optimization algorithms on Bures-Wasserstein manifold, named the Exact Geodesic Gradient Descent and Hybrid Gradient Descent algorithms. While the Exact Geodesic Gradient Descent method is based on computing the exact closed form of the first-order derivative of the objective function of the barycenter along a geodesic on the Bures manifold, the Hybrid Gradient Descent method utilizes optimizer components when solving the SUOT problem to replace outlier measures before applying the Riemannian Gradient Descent. We establish the theoretical convergence guarantees for both methods and demonstrate that the Exact Geodesic Gradient Descent algorithm attains a dimension-free convergence rate. Finally, we conduct experiments to compare the normal Wasserstein Barycenter with ours and perform an ablation study.

RSAM: Learning on manifolds with Riemannian Sharpness-aware Minimization

Nowadays, understanding the geometry of the loss landscape shows promise in enhancing a model's generalization ability. In this work, we draw upon prior works that apply geometric principles to optimization and present a novel approach to improve robustness and generalization ability for constrained optimization problems. Indeed, this paper aims to generalize the Sharpness-Aware Minimization (SAM) optimizer to Riemannian manifolds. In doing so, we first extend the concept of sharpness and introduce a novel notion of sharpness on manifolds. To support this notion of sharpness, we present a theoretical analysis characterizing generalization capabilities with respect to manifold sharpness, which demonstrates a tighter bound on the generalization gap, a result not known before. Motivated by this analysis, we introduce our algorithm, Riemannian Sharpness-Aware Minimization (RSAM). To demonstrate RSAM's ability to enhance generalization ability, we evaluate and contrast our algorithm on a broad set of problems, such as image classification and contrastive learning across different datasets, including CIFAR100, CIFAR10, and FGVCAircraft. Our code is publicly available at \url{https://t.ly/RiemannianSAM}.